lớn nhất = 18

nhỏ nhất = -18

Lớn nhất : 18

          Bé nhất : -18

số lớn nhất có 2 cs là 99 thì a+b=9+9=18

số bé nhất có 2 cs là -99 thì a+b=(-9)+(-9)=-18

Áp dụng bđt \(\frac{m^2}{p}+\frac{n^2}{q}\ge\frac{\left(m+n\right)^2}{p+q}\) được

\(P=\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}=\left(a+b\right)^2\)

Dấu "=" khi ay = bx

Chọn A

Hàm số f(x) = (x-6) x 2 + 4  xác định và liên tục trên đoạn [0;3].

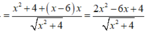
Suy ra 

 với a là số nguyên và b, c là các số nguyên dương nên 

a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.

\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)

Theo bài, a khác b

Nếu muốn các biểu thức nhân, cộng lớn nhất thì các số để nhân,cộng cũng phải lớn nhất

2 số lớn nhất có 1 chữ số là 9 và 8 (a khác b)

Ta có: 9 + 8 = 17 ; 9 x 8 = 72

Vậy giá trị lớn nhất của a + b là 17, của a x b là 72

neu de bai bai 1 la tinh x+y thi mik lam cho

đăng từng này thì ai làm cho 

We have \(P=\frac{x^4+2x^2+2}{x^2+1}\)

\(\Rightarrow P=\frac{x^4+2x^2+1+1}{x^2+1}\)

\(=\frac{\left(x^2+1\right)^2+1}{x^2+1}\)

\(=\left(x^2+1\right)+\frac{1}{x^2+1}\)

\(\ge2\sqrt{\frac{x^2+1}{x^2+1}}=2\)

(Dấu "="\(\Leftrightarrow x=0\))

Vậy \(P_{min}=2\Leftrightarrow x=0\)

a) Vì với mọi giá trị nguyên của x nên

Dấu “=” xảy ra khi x2 = 0 hay x = 0.

Vậy A đạt giá trị nhỏ nhất 2 021 tại x = 0.

b) Vì với mọi giá trị nguyên của x nên với mọi giá trị nguyên của x.

Vì với mọi giá trị nguyên của x nên với mọi giá trị nguyên của x.

Do đó với mọi giá trị nguyên của x.

Suy ra với mọi giá trị nguyên của x.

Dấu “=” xảy ra khi x22 = 0 và x20 = 0 hay x = 0.

Vậy B đạt giá trị lớn nhất bằng 2 022 khi x = 0.