Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm
a) Chứng minh các tứ giác ACC'A, BĐ'B' là hình chữ nhật
b) Chứng minh rằng \(AC'^2=AB^2+AD^2+AA'^2\)
c) Tính diện tích toàn phân và thể tích của hình hộp chữ nhật
Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
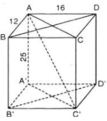
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒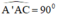 
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=12cm, AD=16cm,AA'=25cm
a) CM các tứ giác ACC'A' , BDD'B'là những hình chữ nhật
b ) CMR AC'2 =AB2 + AD2 +AA'2
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật
a) các tứ giác ACC'A, BDD'B' là hình chữ nhật vì là các mặt bên của hình chữ nhật
b) ta có AC'2=AB2+AD2+AA'2 vì đó là công thức tính đường chéo của hình hộp chữ nhật đã được cm rồi
hoặc bạn có thể tham khảo cm trong sgk
c) diện tích toàn phần của hình hộp chữ nhật là
2*12*16+2*12*15+2*16*15=1224 cm2
thể tích của hình hộp chữ nhật là
12*16*15=2880 cm3
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm. Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D'.
Cho hình hộp chữ nhật ABCD. A'B'C'D' có AB= 12cm, AD= 16cm, AA'= 25cm. Tính diện tích toàn phần và thể tích hình hộp chữ nhật
Diện tích xung quanh:
2 x 25 x (12+16)= 1400(cm2)
Diện tích 2 đáy:
2 x 12 x 16= 384(cm2)
Diện tích toàn phần:
1400+384= 1784(cm2)
Thể tích HHCN:
12 x 25 x 16= 4800(cm3)
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy ABCD là hình vuông, AB=20cm, AA'=19,4cm.
a) Chứng minh tứ giác ABC'D', CDA'B' là hình chũ nhật
b) Tính thể tích và diện tích toàn phần của hình hộp.
Cho hình hộp chũ nhật ABCD.A'B'C'D'. Gọi O là giao điểm của AC' và A'C.
a) Chứng minh B,O,D' thẳng hàng
b) Tính thể tích hình hộp chữ nhật, biết AD=4cm, AB=3cm, BD'=12cm
Cho hình hộp chữ nhật ABCD.ABCD có AB1, BC2, AA3. Mặt phẳng (P) thay đổi và luôn đi qua C’, mặt phẳng (P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Tính tổng TAE+AF+AG sao cho thể tích khối tứ diện AEFG nhỏ nhất. A. 15 B. 16 C. 17 D. 18
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=1, BC=2, AA'=3. Mặt phẳng (P) thay đổi và luôn đi qua C’, mặt phẳng (P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Tính tổng T=AE+AF+AG sao cho thể tích khối tứ diện AEFG nhỏ nhất.
A. 15
B. 16
C. 17
D. 18
Hình hộp chữ nhật ABCD.ABCD có AB a, AD 2a, AA a
2
. Tính thể tích V của ABBD. A. V
a
3
3
2
B. V
2
a
3
2
3
C. V
a
3
2
D. V...
Đọc tiếp
Hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AA' = a 2 . Tính thể tích V của A'BB'D.
A. V = a 3 3 2
B. V = 2 a 3 2 3
C. V = a 3 2
D. V = a 3 2 3
Cho hình hộp chữ nhật ABCD.ABCD. Gọi M, N lần luợt là trung điểm BD và BDa) Nêu vị trí tương đối của các cặp đường thẳng MN và BD; MNvà CC; AC và AD.b) Chứng minh MN ^ (ABCD).c) Biết AA 20 cm,AB 30 cm,AD 40 cm. Tính BD; BM.d) Tính thể tích hình hộp
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi M, N lần luợt là trung điểm BD và B'D'
a) Nêu vị trí tương đối của các cặp đường thẳng MN và BD; MNvà CC'; AC và A'D'.
b) Chứng minh MN ^ (A'B'C'D').
c) Biết AA' = 20 cm,AB = 30 cm,AD = 40 cm. Tính B'D'; B'M.
d) Tính thể tích hình hộp
a) Ta có MN cắt BD tại M.
MN//CC', AC và A'D' chéo nhau.
b) MN ^ A'C' và B'D'
c) B'S' = 50cm, B'M = 5 41 c m
d) V =24000cm3
Đúng 0
Bình luận (0)