Hãy vẽ phác một lục giác lồi
Hãy nêu các nhận biết một đa giác lồi
Hãy vẽ phác một lục giác lồi.
Hãy nêu cách nhận biết một đa giác lồi.
- Lục giác lồi ABCDEF
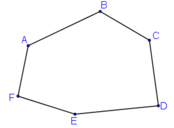
- Cách nhận biết một đa giác lồi:
Lần lượt xét các nửa mặt phẳng bờ là cạnh của đa giác, nếu đa giác luôn nằm hoàn toàn trong một nửa mặt phẳng thì đa giác là đa giác lồi.
Nếu có 1 cạnh mà đa giác nằm trên cả hai nửa mặt phẳng mà đường thẳng chứa cạnh là bờ thì đa giác không phải đa giác lồi.
1 hãy vẽ phác một lục giác lồi.
2 hãy nêu cách nhận biết một lục giác lồi.
Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình.
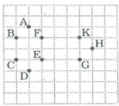
Cho hai hình vuông bất kì. Hãy cắt hai hình vuông thành các đa giác lồi và xếp các đa giác lồi thành một hình vuông.
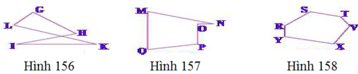
Xem các hình 156, 157, 158 và trả lời các câu hỏi sau:
a) Vì sao hình năm cạnh GHIKL (h.156) không phải là đa giác lồi?
b) Vì sao hình năm cạnh MNOPQ (h.157) không phải là đa giác lồi?
c) Vì sao hình sáu cạnh RSTVXY (h.158) là một đa giác lồi?
Hãy phát biểu định nghĩa đa giác lồi.
a) + b) Đa giác GHIKL và MNOPQ không phải là đa giác lồi vì không nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
c) Đa giác RSTVXY là đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
- Định nghĩa:
Đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Xem các hình 156, 157, 158 và trả lời các câu hỏi sau :
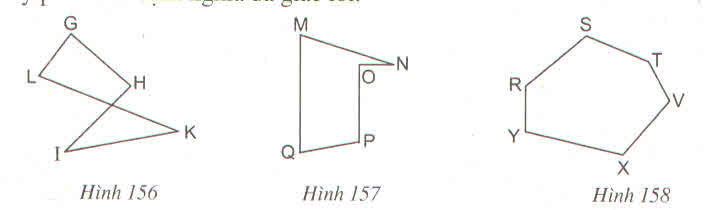
a) Vì sao hình năm cạnh GHIKL (h.156) không phải là đa giác lồi ?
b) Vì sao hình năm cạnh MNOPQ (h.157) không phài là đa giác lồi ?
c) Vì sao hình sáu cạnh RSTVXY (h.158) là một đa giác lồi ?
Hãy phát biểu định nghĩa đa giác lồi ?
Tham khảo:
a) + b) Đa giác GHIKL và MNOPQ không phải là đa giác lồi vì không nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
c) Đa giác RSTVXY là đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
- Định nghĩa:
Đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Hãy vẽ một số đa giác lồi mà các đỉnh là một số điểm trong các điểm đã cho ở hình dưới :

Cho n,k là số nguyên dương .xét một đa giác lồi n cạnh,n > hoặc = 5.Người ta muốn kẻ một số đường chéo của đa giác mà các đường chéo này chia các đa giác đã cho thành đúng k miền,mỗi miền là một ngũ giác lồi(hai miền bất kì Ko có điểm chung nào).
A)với n=2017,k=672 ta có thể thực hiện được Ko?hãy giải thích
Một đa giác lồi \(n\) cạnh được chia thành các tam giác bằng cách vẽ \(n-3\) đường chéo đôi một không cắt nhau ở bên trong đa giác. Biết rằng ở mỗi đỉnh có một số lẻ các tam giác nhỏ. CMR \(n⋮3\)
Để chứng minh rằng một đa giác lồi có n cạnh, khi được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3, ta có thể sử dụng phương pháp quy nạp (induction) để giải quyết bài toán này.
Đầu tiên, chúng ta xét trường hợp đơn giản nhất khi n = 3, tức là đa giác là tam giác. Trong trường hợp này, không cần vẽ đường chéo nào cả, vì tam giác đã được chia thành các tam giác bằng nhau. Và n = 3 chia hết cho 3.
Giả sử đa giác có n cạnh thỏa mãn điều kiện trong đề bài. Ta sẽ chứng minh rằng khi thêm một cạnh mới vào đa giác, tức là n+1 cạnh, thì n+1 cũng phải chia hết cho 3.
Giả sử đa giác có n cạnh và đã được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau. Khi thêm một cạnh mới vào đa giác, chúng ta sẽ thêm một tam giác mới và tạo ra một đường chéo mới. Khi đó, số tam giác trong đa giác tăng thêm một đơn vị và số đường chéo tăng thêm một đơn vị.
Điều quan trọng là ta phải đảm bảo rằng khi thêm một cạnh mới vào, chúng ta vẫn có thể chia đa giác thành các tam giác bằng nhau bằng cách vẽ n-2 đường chéo đôi một không cắt nhau. Điều này có nghĩa là ta cần thêm một đường chéo mới để duy trì tính chất của đa giác ban đầu.
Với việc thêm một cạnh mới, số đường chéo tăng lên một đơn vị, nên ta cần có (n-2)+1 = n-1 đường chéo. Điều này đồng nghĩa với việc n-1 phải chia hết cho 3.
Dựa trên quy nạp, chúng ta có thể kết luận rằng với mọi số tự nhiên n ≥ 3, nếu đa giác có n cạnh và được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3.
Vậy, điều phải chứng minh đã được chứng minh.