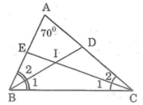
Trong ∆ABC, ta có:

∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)

Suy ra: ∠B + ∠C = 180o - ∠A = 180o - 70o = 110o

Ta có:

∠(B1 ) = 1/2 ∠B (vì BD là tia phân giác)

∠(C1 ) = 1/2 ∠C (vì CE là tia phân giác)

Trong ∆BIC, ta có:

∠(BIC) + ∠(B1 ) + ∠(C1 ) = 180o (tổng 3 góc trong tam giác)

Suy ra: ∠(BIC) = 180o - (∠(B1 ) + ∠(C1)) = 180o - 1/2 (∠B + ∠C)

= 180o - 1/2 .110o = 125o

câu a : Bạn áp dụng định lý py - ta - go đảo nhá ^^
câu b : Có BD là phân giác \(\widehat{ABC}\), CE là phân giác \(\widehat{ACB}\)

\(\Rightarrow\)\(\widehat{IBC}=\frac{1}{2}\widehat{ABC}\), \(\widehat{ICB}=\frac{1}{2}\widehat{ACB}\)
\(\Rightarrow\)\(\widehat{IBC}+\widehat{ICB}=\frac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=\frac{1}{2}90=45\)

a;\(6^2+8^2=100\)

\(10^2=100\)

\(\Rightarrow6^2+8^2=10^2\)

=> Tam giác có đọ dài 3 cạnh lần lượt là 6cm;8cm;10;cm là tam giác vuông

Cho tam giác MNP cân tại P ( P là góc nhọn),vẽ MA vuông góc với PN tại A,NC vuông góc với PM tại C

Chứng minh : PC=PA và CA// MN 

Gọi I là giao điểm MA và NC.Tia PI cắt MN tại K .Chứng minh K là trung điểm MN

Ta có ∠(ACB) = 180o - 70o - 30o = 80o

Do CI là tia phân giác của góc ACB nên ∠(ACI) = 80o : 2 = 40o. Chọn C

Trong tam giác BIC có ∠(BIC) + ∠(IBC) + ∠(ICB) = 180o ⇒ (IBC) + (ICB) = 60o

∠(ABC) + ∠(ACB) = 2∠(IBC) + 2∠(ICB) = 2(∠(IBC) + ∠(ICB) ) = 2.60o = 120o

Có ∠A = 180o - 120o = 60o. Chọn A

(Bạn tự vẽ hình giùm)

Ta có \(\widehat{IBC}=\frac{\widehat{ABC}}{2}\)(BD là tia phân giác của \(\widehat{ABC}\))

và \(\widehat{ICB}=\frac{\widehat{ACB}}{2}\)(CE là tia phân giác của \(\widehat{ACB}\))

=> \(\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}\)

=> \(180^o-\widehat{BIC}=\frac{180^o-\widehat{A}}{2}\)

=> \(180^o-\widehat{BIC}=90^o-\frac{\widehat{A}}{2}\)

=> \(180^o-90^o=\widehat{BIC}-\frac{\widehat{A}}{2}\)

=> \(\widehat{BIC}-\frac{\widehat{A}}{2}=90^o\)

=> \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\)

Thay \(\widehat{A}=80^o\)vào biểu thức \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\), ta có:

\(\widehat{BIC}=90^o+\frac{80^o}{2}\)

=> \(\widehat{BIC}=90^o+40^o=130^o\)

Ta có ^IBC=^ABC2 (BD là tia phân giác của ^ABC)

và ^ICB=^ACB2 (CE là tia phân giác của ^ACB)

=> ^IBC+^ICB=^ABC+^ACB2 

=> 180o−^BIC=180o−^A2 

=> 180o−^BIC=90o−^A2 

=> 180o−90o=^BIC−^A2 

=> ^BIC−^A2 =90o

=> ^BIC=90o+^A2 

Thay ^A=80ovào biểu thức ^BIC=90o+^A2 , ta có:

^BIC=90o+80o2 

=> ^BIC=90o+40o=130o

Ta có ^IBC=^ABC2 (BD là tia phân giác của ^ABC)

và ^ICB=^ACB2 (CE là tia phân giác của ^ACB)

=> ^IBC+^ICB=^ABC+^ACB2 

=> 180o−^BIC=180o−^A2 

=> 180o−^BIC=90o−^A2 

=> 180o−90o=^BIC−^A2 

=> ^BIC−^A2 =90o

=> ^BIC=90o+^A2 

Thay ^A=80ovào biểu thức ^BIC=90o+^A2 , ta có:

^BIC=90o+80o2 

=> ^BIC=90o+40o=130o

Trong tam giác ABC có:

∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o

Mà BI và CI lâ các tia phân giác nên

∠(ABC) + ∠(ACB) = 2.∠(IBC) + 2.∠(ICB) = 2 (∠(IBC) + ∠(ICB) )

Suy ra ∠(IBC) + ∠(ICB) = 50o

Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o. Chọn C

t ko bt lm r :))

BIC = 130^o

\(\widehat{ABC}+\widehat{ACB}=180-80=100\)

\(=>\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{100}{2}=50\)

\(=>\widehat{BIC}=180-\left(\widehat{IBC}+\widehat{ICB}\right)=180-50=130\)

okey nhé bợn

Xét tam giác ABC có góc B+C=180 độ- góc A =180-80=100 độ

Vì BI và CI lần lượt là tia phân giác của góc B,C

Nên góc IBC+ICB =1/2B+1/2C=1/2(B+C)=1/2*100=50 độ

xét tam giác IBC có góc I=180 độ -(góc IBC+ICB)=180-50=130độ

vậy goác IBC bằng 130 độ

mình hơi bận nên không có thời gian trình bày cho bạn nên bạn nhớ trình bày lại nhé ,còn cái này thì mình chỉ giai thích cho bạn hiểu thôi .