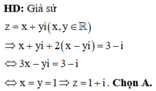Tìm các số phức \(2z+\overline{z}\) và \(\dfrac{25i}{z}\) biết rằng \(z=3-4i\)

Những câu hỏi liên quan
Tìm các số phức 2z +
z
và 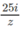 biết rằng z = 3 – 4i
biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
2z + z = 2(3 − 4i) + 3 + 4i = 6 − 8i + 3 + 4i = 9 − 4i
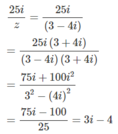
Đúng 0
Bình luận (0)
Tìm các số phức 2z + z ¯ và 25 i z biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
2z + z ¯ = 2(3 − 4i) + 3 + 4i = 6 − 8i + 3 + 4i = 9 − 4i
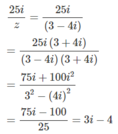
Đúng 0
Bình luận (0)
Biết các số phức z thỏa mãn |z-3||z+4i|. Tìm
w
m
i
n
biết w z + 4i -3 A.
w
m
i
n
7
5
B.
w
m
i
n
...
Đọc tiếp
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7
Tìm số phức \(z\) biết
a) \(\overline{z}=z^3\)
b) \(\left|z\right|+z=3+4i\)
Tìm số phức z thỏa mãn
z
+
2
z
¯
2
-
4
i
Đọc tiếp
Tìm số phức z thỏa mãn z + 2 z ¯ = 2 - 4 i
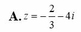
![]()
![]()
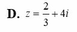
Cho số phức z thỏa mãn
z
+
3
−
4
i
5.
Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó. A.
I
3
;
−
4
,
R
5...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 − 4 i = 5. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó.
A. I 3 ; − 4 , R = 5 .
B. I − 3 ; 4 , R = 5 .
C. I 3 ; − 4 , R = 5.
D. I − 3 ; 4 , R = 5.
Đáp án D.
Phương pháp:
Gọi z = a + b i , sử dụng công thức tính môđun của số phức.
Cách giải:
Giả sử z = x + y i , x , y ∈ R
Theo đề bài ta có:
z + 3 − 4 i = 5 ⇔ x + 3 2 + y − 4 2 = 5 ⇔ x + 3 2 + y − 4 2 = 25
Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm I − 3 ; 4 , R = 5.
Đúng 0
Bình luận (0)
bài 1 a/tìm số phức z biết left|zright|+z3+4ib/ cho các số phức z1 z2 thỏa mãn z1+3z1z2(-1+i)z2 và 2z1-z23+2i.tìm modun của số phức wfrac{z1}{z2}+z1+z2bài 2 a/giải pt trên tập số phức 2z^4-7z^3+9z^2+20b/cho số phức z1+isqrt{3}.Hãy tìm dạng lượng giác của các số phức z , overline{z} , -z,frac{1}{z}
Đọc tiếp
bài 1 a/tìm số phức z biết \(\left|z\right|+z=3+4i\)
b/ cho các số phức z1 z2 thỏa mãn z1+3z1z2=(-1+i)z2 và 2z1-z2=3+2i.tìm modun của số phức w=\(\frac{z1}{z2}\)+z1+z2
bài 2 a/giải pt trên tập số phức 2\(z^4\)-7\(z^3\)+9\(z^2\)+2=0
b/cho số phức z=1+i\(\sqrt{3}\).Hãy tìm dạng lượng giác của các số phức z , \(\overline{z}\) , -z,\(\frac{1}{z}\)
Tìm số phức z biết rằng
z
+
2
z
¯
3
-
i
A.
z
1
+
i
B.
z
1
-
1
3
i
C.
z
-
1
+
i
D.
z
-
1
-
i
Đọc tiếp
Tìm số phức z biết rằng z + 2 z ¯ = 3 - i
A. z = 1 + i
B. z = 1 - 1 3 i
C. z = - 1 + i
D. z = - 1 - i
Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:
\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.