Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820 ?

Những câu hỏi liên quan
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820?
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
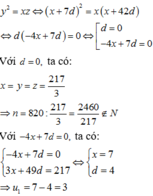
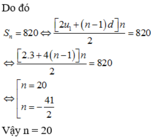
Đúng 0
Bình luận (0)
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng A. 21 B. 42 C.20 D. 17
Đọc tiếp
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Ba số khác nhau có tổng bằng 114 có thể coi là ba số hạng liên tiếp của một cấp số nhân, hoặc coi là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng. Tìm các số đó ?
Gọi 3 số đó là: \(a,b,c\). Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=114\\b^2=ac\end{matrix}\right.\). (*)
Mặt khác nó lần lượt là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng nên: \(a=u_1;b=u_1+3d;c=u_1+24d\). ( với \(u_1\) là số hạng đầu của cấp số cộng, d là công sai).
Thay vào (*) ta có:
\(\left\{{}\begin{matrix}u_1+u_1+3d+u_1+24d=114\\\left(u_1+3d\right)^2=u_1\left(u_1+24d\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\18u_1d-9d^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\9d\left(2u_1-d\right)=0\end{matrix}\right.\).
Nếu \(d=0\) thì a,b,c là ba số hạng của một cấp số cộng không đổi nên \(a=b=c=\sqrt[3]{114}\).
Nếu \(d\ne0\) suy ra: \(\left\{{}\begin{matrix}u_1+9d=38\\2u_1-d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=2\\d=4\end{matrix}\right.\).
Khi đó \(a=2;b=2+3.4=16;c=2+24.3=74\).
Đúng 0
Bình luận (0)
Một cấp số cộng và một cấp số nhân đều là các dãy tăng. Các số hạng thứ nhất đều bằng 3, các số hạng thứ hai bằng nhau. Tỉ số giữa số hạng thứ ba của cấp số nhân và cấp số cộng là 9/5. Tính tổng các số hạng thứ ba của hai cấp số trên. A. 29. B. 24. C. 18. D. 42.
Đọc tiếp
Một cấp số cộng và một cấp số nhân đều là các dãy tăng. Các số hạng thứ nhất đều bằng 3, các số hạng thứ hai bằng nhau. Tỉ số giữa số hạng thứ ba của cấp số nhân và cấp số cộng là 9/5. Tính tổng các số hạng thứ ba của hai cấp số trên.
A. 29.
B. 24.
C. 18.
D. 42.
Một cấp số cộng và một cấp số nhân đều là các dãy số tăng. Các số hạng thứ nhất đều bằng 3, các số hạng thứ hai bằng nhau, tỷ số giữa các số hạng thứ ba của cấp số nhân và cấp số cộng là 9/5. Tính tổng S của cấp số nhân đó
A. S= 27
B. S= 39
C. S= 29
D. S= 37
Một cấp số cộng và một cấp số nhân có số hạng thứ nhất bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ ba bằng nhau. Tìm các cấp số ấy.
ĐS: Cấp số cộng: 5, 25, 45
Cấp số nhân: 5, 15, 45
Đúng 0
Bình luận (0)
Một cấp số cộng và một cấp số nhân có số hạng thứ nhất bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ 3 bằng nhau. Tìm các cấp số ấy ?
Gọi 3 số hạng của cấp số cộng là: \(5;5+d;5+2d\)
Gọi 3 số hạng của cấp số nhân là: \(5;5q;5q^2\).
Ta có hệ sau:\(\left\{{}\begin{matrix}5+2d=5q^2\\5+d=5q+10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5+2d=5q^2\\d=5q+5\end{matrix}\right.\)\(\Rightarrow5+2.\left(5q+5\right)=5q^2\)\(\Rightarrow\left\{{}\begin{matrix}q=-1\\q=3\end{matrix}\right.\).
Với \(q=-1\) thì \(d=5.q+5=5.\left(-1\right)+5=0\).
Với \(q=3\) thì \(d=5.q+5=5.3+5=20\).
Vậy
Với \(q=-1\):
3 số hạng của cấp số cộng là: 5; 5; 5.
3 số hạng của cấp số nhân là: 5; - 5; 5.
Với \(q=3\):
3 số hạng của cấp số cộng là: 5; 25; 45.
3 số hạng của cấp số nhân là: 5; 15; 45.
Đúng 0
Bình luận (0)
Tìm số hạng đầu của cấp số nhân có bốn số hạng, biết tổng ba số hạng đầu bằng 16 4 9 , đồng thời theo thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.
A. 4
B. 16/9
C. 2/3
D. -1
Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4
Đúng 0
Bình luận (0)






