giai pt:|z| + z=3+4i

Những câu hỏi liên quan
Biết các số phức z thỏa mãn |z-3||z+4i|. Tìm
w
m
i
n
biết w z + 4i -3 A.
w
m
i
n
7
5
B.
w
m
i
n
...
Đọc tiếp
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7
Giai pt nghiệm nguyên dương : x^3-y^3-z^3=3xyz và x^2=2.(y+z)
Làm đúng mk sẽ tick
1...Chia cả hai vế cho xyz ta được
3xy/xyz + 3yz/xyz + 3zx/xyz = 4xyz/xyz
<=>3/x + 3/y + 3/z = 4
<=>1/x + 1/y + 1/z = 4/3
Vì x,y,z bình đẳng nên giả sử 0<x<=y<=z
+nếu x>=4=> y>=4;z>=4
=> 1/x + 1/y + 1/z <= 1/4 + 1/4 + 1/4 =3/4 < 4/3 => pt vô nghiệm
+nếu x=1 => 1+1/y+1/z=4/3
<=> 1/y+1/z=1/3
<=> 3(y+z)=yz
<=> 3y+3z-yz=0
<=> 3y-yz+3z-9=-9
<=> y(3-z)-3(3-z)=-9
<=> (3-z)(3-y)=9
Vì y,z nguyên dương nên (3-y),(3-z) nguyên dương
mà 9=3*3=1*9=9*1
==>3-z=3 và 3-y=3 => z=0 và y=0 (loại vì y,z nguyên dương)
+nếu x=2 => 1/2+1/y+1/z=4/3
<=> 1/y+1/z=5/6
<=> 6(y+z)=5yz
<=> 6y+6z-5yz=0
<=> 30y-25yz+30z-36=-36
<=> 5y(6-5z)-6(6-5z)=-36
<=> (5z-6)(5y-6)=36
Vì y,z nguyên dương nên (5y-6),(5z-6) nguyên dương
mà 36=6*6=2*18=18*2=3*12=12*3=4*9=9*4
Giải tương tự phần trên ta được
y=2,z=3 hoặc y=3,z=2
+nếu x=3 => 1/3+1/y+1/z=4/3
<=> 1/y+1/z=1
Giải tương tự phần trên ta được y=z=2
Vậy (x;y;z)=(2;2;3);(2;3;2);(3;2;2)
Đây là bài gần giống nhé
Đúng 0
Bình luận (0)
z, z1, z2, z3 thuộc C thỏa |z|=|z1|=|z2|=|z3|=10 (z1#z2#z3)
(z-3+4i)(thanh ngang của (z1-z2)); (z-3+4i)(thanh ngang của (z2-z3)); (z-3+4i)(thanh ngang của (z3-z1)) là thuần ảo
Tìm max P= |z-z1|^2+|z-z2|^2+|z-z3|^2
Ai cứu mình với!
Giai pt nghiệm nguyên dương : x^3 - y^3 - z^3 = 3 . xyz và x^2 = 2 . ( y+z )
Ai giải đúng mk cho 3 tick luôn nha
mk ms hok lp 6 thoy nên ko biết làm
tk mk nha
chúc các bn hok tốt !
Đúng 0
Bình luận (0)
\(x^3-\left(y^3+z^3\right)=3xyz\)
\(\Rightarrow x^3-\left[\left(y+z\right)^3-3yz\left(y+z\right)\right]=3xyz\)
\(\Rightarrow x^3-\left(y+z\right)^3+3yz\left(y+z\right)=3xyz\)
\(\Rightarrow x^3-\left(y+z\right)^3=3yz\left[x-\left(y+z\right)\right]\)
\(\Rightarrow\left[x-\left(y+z\right)\right]\left[x^2+x\left(y+z\right)+\left(y+z\right)^2-3yz\right]=0\)
\(\Rightarrow\left[x-\left(y+z\right)\right]\left[x^2+x\left(x+y\right)+y^2+z^2-yz\right]=0\)
Mà \(x^2+x\left(x+y\right)+y^2+z^2-yz>0\)
\(\Rightarrow x=y+z\)
\(\Rightarrow\left(y+z\right)^2=2\left(y+z\right)\)
\(\Rightarrow\left(y+z\right)^2-2\left(y+z\right)=0\)
\(\Rightarrow\left(y+z\right)\left(y+z-2\right)=0\)
\(\Rightarrow\hept{\begin{cases}y=z=1\\x=2\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giai pt nghiệm nguyên dương : x^3-y^3-z^3=3xyz và x^2=2.(y+z)
Ai làm nhanh và đúng nhất mk tick cho ; đang cần gấp
Tìm số phức z, biết: z + z = 3 + 4 i
Đặt z = a + bi. Từ z + z = 3 + 4 i suy ra
![]()
![]()
⇒ a 2 + 16 = 3 - a 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
Đúng 0
Bình luận (0)
Tìm số phức z, biết:
a) z = z 3 ;
b) |z| + z = 3 + 4i.
a) Ta có z. z = z 2 nên từ z = z 3 ⇒ z 2 = z 4
Đặt z = a+ bi , suy ra:
a 4 + b 4 − 6 a 2 b 2 + 4ab( a 2 − b 2 )i = a 2 + b 2 (∗)
Do đó, ta có: 4ab( a 2 − b 2 ) = 0 (∗∗)
Từ (∗∗) suy ra các trường hợp sau:
+) a = b = 0 ⇒ z = 0
+) a = 0, b ≠ 0: Thay vào (∗), ta có b 4 = b 2 ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1
+) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1
+) a ≠ 0, b ≠ 0 ⇒ a 2 − b 2 = 0⇒ a 2 = b 2 , thay vào (∗) , ta có:
2 a 2 (2 a 2 + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )
b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra
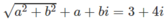
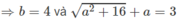
⇒ a 2 + 16 = ( 3 - a ) 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
Đúng 0
Bình luận (0)
Giai pt nghiệm nguyên dương : x^3-y^3-z^3=3xyz và x^2=2.(y+z)
Làm nhanh nha các bạn
Ai làm đúng thì sẽ được tik
sory bn
mk ms hok lp 6
chúc các bn hok tốt !
Đúng 0
Bình luận (0)
Tìm min của Y= 3|Z|+4|Z-4i|+5|Z-3|
đặc \(z=a+bi\) (\(a;b\in R\) và \(i^2=-1\))
ta có : \(Y=3\left|z\right|+4\left|z-4i\right|+5\left|z-3\right|\)
\(\Leftrightarrow Y=3\left|a+bi\right|+4\left|a+\left(b-4\right)i\right|+5\left|\left(a-3\right)+bi\right|\)
\(\Leftrightarrow Y=3\sqrt{a^2+b^2}+4\sqrt{a^2+\left(b-4\right)^2}+5\sqrt{\left(a-3\right)^2+b^2}\)
áp dụng bất đẳng thức Bunhiacopxki ta có :
\(Y\ge-\sqrt{\left(3^2+4^2+5^2\right)\left(a^2+b^2+a^2+\left(b-4\right)^2+\left(a-3\right)^2+b^2\right)}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3a^2+3b^2-8b-6a+25}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3\left(a-1\right)^2+\left(\sqrt{3}b-\dfrac{8}{2\sqrt{3}}\right)^2+\dfrac{50}{3}}\)
dấu "=" xảy ra khi \(\dfrac{3}{\sqrt{a^2+b^2}}=\dfrac{4}{\sqrt{a^2+\left(b-4\right)^2}}=\dfrac{4}{\sqrt{\left(a-3\right)^2}+b^2}\)
giải ra tìm được \(a;b\) rồi thay ngược trở lại nha
Đúng 0
Bình luận (0)












