Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:
\(\dfrac{3}{\sqrt{3}+1};\dfrac{2}{\sqrt{3}-1};\dfrac{2+\sqrt{3}}{2-\sqrt{3}};\dfrac{b}{3+\sqrt{b}};\dfrac{p}{2\sqrt{p}-1}.\)
Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:
\(\dfrac{2}{\sqrt{6}-\sqrt{5}};\dfrac{3}{\sqrt{10}+\sqrt{7}};\dfrac{1}{\sqrt{x}-\sqrt{y}};\dfrac{2ab}{\sqrt{a}-\sqrt{b}}.\)
\(\dfrac{2ab}{\sqrt{a}-\sqrt{b}}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)
\(\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}+\sqrt{7}\right)\left(\sqrt{10}-\sqrt{7}\right)}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{3}=\sqrt{10}-\sqrt{7}\)
\(\dfrac{2}{\sqrt{6}-\sqrt{5}}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)
Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:
\(\dfrac{5}{\sqrt{10}};\dfrac{5}{2\sqrt{5}};\dfrac{1}{3\sqrt{20}};\dfrac{2\sqrt{2}+2}{5\sqrt{2}};\dfrac{y+b\sqrt{y}}{b.\sqrt{y}}.\)
Nhat Linh bị nhầm câu cuối:
\(\dfrac{y+b\sqrt{y}}{b.\sqrt{y}}=\dfrac{y\sqrt{y}+b.y}{b.y}=\dfrac{\sqrt{y}+b}{b}.\)
Bài 51 (trang 30 SGK Toán 9 Tập 1)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
$\dfrac{3}{\sqrt{3}+1}$ ; $\dfrac{2}{\sqrt{3}-1}$; $\dfrac{2+\sqrt{3}}{2-\sqrt{3}}$ ; $\dfrac{b}{3+\sqrt{b}}$ ; $\dfrac{p}{2 .\sqrt{p}-1}$.
33+1=3(3−1)(3+1)(3−1)=33−3.1(3)2−12" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
33−33−1=33−32" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
23−1=2(3+1)(3−1)(3+1)=2(3+1)(3)2−12" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
2(3+1)3−1=2(3+1)2=3+1" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
2+32−3=(2+3).(2+3)(2−3)(2+3)=(2+3)222−(3)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
22+2.2.3+(3)24−3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
7+431=7+43" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
b3+b=b(3−b)(3+b)(3−b)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
b(3−b)32−(b)2=b(3−b)9−b;(b≠9)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
p2p−1=p(2p+1)(2p−1)(2p+1)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
p(2p+1)(2p)2−12=p(2p+1)4p−1" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
#Ye Chi-Lien
\(\frac{3}{\sqrt{3}+1}=\frac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\frac{3\sqrt{3}-3}{3-1}=\frac{3\sqrt{3}-3}{2}\)
\(\frac{2}{\sqrt{3}-1}=\frac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\frac{2\left(\sqrt{3}+1\right)}{3-1}=\sqrt{3}-1\)
\(\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{\left(2+\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3}=\left(2+\sqrt{3}\right)^2=4+4\sqrt{3}+3=7+4\sqrt{3}\)
\(\frac{b}{3+\sqrt{b}}=\frac{b\left(3-\sqrt{b}\right)}{\left(3+\sqrt{b}\right)\left(3-\sqrt{b}\right)}=\frac{b\left(3-\sqrt{b}\right)}{9-b}\)
\(\frac{p}{2\sqrt{p}-1}=\frac{p\left(2\sqrt{p}+1\right)}{\left(2\sqrt{p}-1\right)\left(2\sqrt{b}+1\right)}=\frac{p\left(2\sqrt{b}+1\right)}{4p-1}\)
+) .
+) .
+) .
+) .
+)
Bài 52 (trang 30 SGK Toán 9 Tập 1)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
$\dfrac{2}{\sqrt{6}-\sqrt{5}}$ ; $\dfrac{3}{\sqrt{10}+\sqrt{7}}$ ; $\dfrac{1}{\sqrt{x}-\sqrt{y}}$ ; $\dfrac{2 a b}{\sqrt{a}-\sqrt{b}}$.
+ Ta có:
2√6−√5=2(√6+√5)(√6−√5)(√6+√5)26−5=2(6+5)(6−5)(6+5)
=2(√6+√5)(√6)2−(√5)2=2(√6+√5)6−5=2(6+5)(6)2−(5)2=2(6+5)6−5
=2(√6+√5)1=2(√6+√5)=2(6+5)1=2(6+5).
+ Ta có:
3√10+√7=3(√10−√7)(√10+√7)(√10−√7)310+7=3(10−7)(10+7)(10−7)
=3(√10−√7)(√10)2−(√7)2=3(10−7)(10)2−(7)2=3(√10−√7)10−7=3(10−7)10−7
=3(√10−√7)3=√10−√7=3(10−7)3=10−7.
+ Ta có:
1√x−√y=1.(√x+√y)(√x−√y)(√x+√y)1x−y=1.(x+y)(x−y)(x+y)
=√x+√y(√x)2−(√y)2=√x+√yx−y=x+y(x)2−(y)2=x+yx−y
+ Ta có:
2ab√a−√b=2ab(√a+√b)(√a−√b)(√a+√b)2aba−b=2ab(a+b)(a−b)(a+b)
=2ab(√a+√b)(√a)2−(√b)2=2ab(√a+√b)a−b=2ab(a+b)(a)2−(b)2=2ab(a+b)a−b.
\(\frac{2}{\sqrt{6}-\sqrt{5}}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)
\(\frac{3}{\sqrt{10}+\sqrt{7}}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}-\sqrt{7}\right)\left(\sqrt{10}+\sqrt{7}\right)}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\sqrt{10}-\sqrt{7}\)
\(\frac{1}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\frac{2ab}{\sqrt{a}-\sqrt{b}}=\frac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)
Bài 50 (trang 30 SGK Toán 9 Tập 1)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
$\dfrac{5}{\sqrt{10}}$; $\dfrac{5}{2 \sqrt{5}}$ ; $\dfrac{1}{3 \sqrt{20}}$ ; $\dfrac{2 \sqrt{2}+2}{5 \sqrt{2}}$ ;$\dfrac{y+b.\sqrt{y}}{b.\sqrt{y}}$.
\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{5}{2\sqrt{5}}=\frac{10\sqrt{5}}{20}=\frac{\sqrt{5}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{3\sqrt{20}}{180}=\frac{\sqrt{20}}{60}=\frac{2\sqrt{5}}{60}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{10\sqrt{2}\left(\sqrt{2}+1\right)}{50}=\frac{20+10\sqrt{2}}{50}=\frac{10\left(2+\sqrt{2}\right)}{50}=\frac{2+\sqrt{2}}{5}\)
\(\frac{y+b\sqrt{y}}{b\sqrt{y}}=\frac{y\left(\sqrt{y}+b\right)}{by}=\frac{\sqrt{y}+b}{b}\)
510=5.1010.10=510(10)2=51010" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
5.105.2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
525=5.525.5=552.(5.5)=552(5)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
552.5=52" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
1320=1.20320.20=203.(20.20)=203.(20)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
203.20=22.560=2560=252.30=530" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
(22+2)5.2=(22+2).252.2=22.2+2.25.(2)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
2.2+225.2=2(2+2)5.2=2+25" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
y+byby=(y+by).yby.y=yy+by.yb.(y)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
yy+b(y)2by=yy+byby" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
y(y+b)b.y=y+bb" role="presentation" style="border:0px; direction:ltr; display:inline-table; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
y+byby=(y)2+byby" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
Nguồn : Bài 50 trang 30 SGK Toán 9 tập 1 - loigiaihay.com
#Ye Chi-Lien
\(\dfrac{5}{\sqrt{10}}=\dfrac{\sqrt{10}}{2}\)
\(\dfrac{5}{2\cdot\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)
\(\dfrac{1}{3\cdot\sqrt{20}}=\dfrac{\sqrt{20}}{60}\) ;
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa 3 3 + 1 ; 2 3 - 1 ; 2 + 3 2 - 3 ; b 3 + b ; p 2 p - 1
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
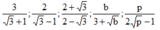
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
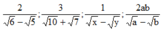
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
5 10 ; 5 2 5 ; 1 3 20 ; 2 2 + 2 5 2 ; y + b y b y