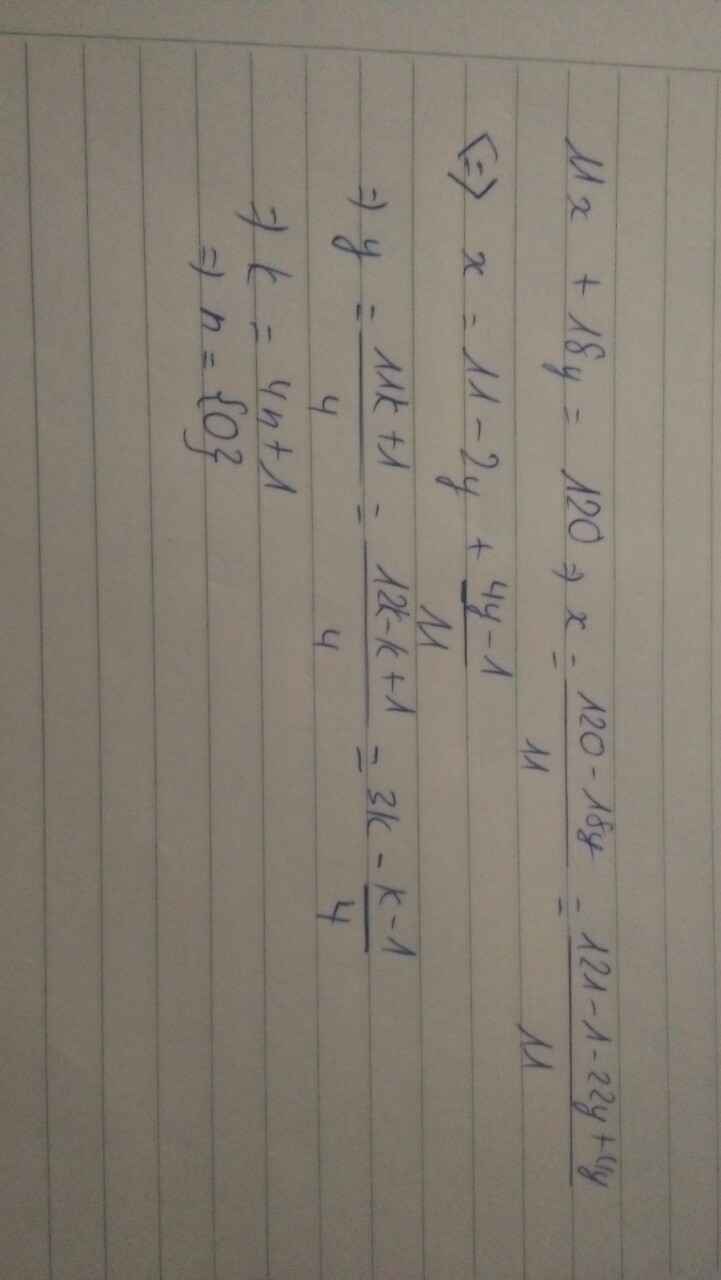y = 7 - 4k +k - 13 Lại đặt k - 13 = t với t nguyên => k = 3t + 1 . Do đó : = 7 - 4 ( 3t + 1) +t = 3 - 11 = tx = 6k = 6 ( 3t+1) = 18t + 6 Thay các biểu thức của x và y vào (1), phương trình đượ c nghiệm đúng. Vậy các nghiệm nguyên của (1) đượ c biểu thị bở i công thức : {=18t+6y=3−11t vớ i t là số nguyên tùy ý mk nha các bạn !!! 

\(11x+18y=120\Rightarrow x=\dfrac{120-18y}{11}=\dfrac{121-1-22y+4y}{11}\)\(\Leftrightarrow x=11-2y+\dfrac{4y-1}{11}\)

\(\left\{{}\begin{matrix}\dfrac{4y-1}{11}=k\\11k=4y-1\end{matrix}\right.\) \(\Rightarrow y=\dfrac{11k+1}{4}=\dfrac{12k-k+1}{4}=3k-\dfrac{k-1}{4}\)

\(\left\{{}\begin{matrix}\dfrac{k-1}{4}=n\\4n=k-1\end{matrix}\right.\) \(\Rightarrow k=4n+1\)

\(\Rightarrow\left\{{}\begin{matrix}y=3.\left(4n+1\right)-n=11n+3\\x=11-2\left(11n+3\right)+4n+1=6-18n\end{matrix}\right.\)

\(x,y>0\Rightarrow\left\{{}\begin{matrix}6-18n>0\\11n+3>0\end{matrix}\right.\) \(\left\{{}\begin{matrix}n< \dfrac{6}{18}\\n>\dfrac{-3}{11}\end{matrix}\right.\) \(\Rightarrow n=\left\{0\right\}\)

Nghiệm duy nhất của phương trình là:

\(\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\)

mk k biet xin loi ban nha!!!!!

mk k biet xin loi ban nha!!!!!

mk k biet xin loi ban nha!!!!!

mk k biet xin loi ban nha!!!!!

http://www.slideshare.net/hoanghoanhao18/9-phng-php-gii-phng-trnh-nghim-nguyn

tìm các số nguyên dương x,y thỏa mãn 11x+18y=120

Tích mk nha các bạn 

\(11x+18y=120\)

Có: \(18y⋮6,120⋮6\Rightarrow11x⋮6\Rightarrow x⋮6\)

Đặt \(x=6k\), ta được: \(11k+3y=20\Rightarrow y=\frac{20-11k}{3}=7-4k+\frac{k-1}{3}\)

Đặt \(\frac{k-1}{3}=t\left(t\inℤ\right)\Rightarrow k=3t+1\)

\(\Rightarrow\hept{\begin{cases}y=7-4\left(3t+1\right)=3-11t\\x=6k=18t+6\end{cases}}\)

=>Các nghiệm nguyên của phương trình là :

\(\hept{\begin{cases}x=18t+6\\y=3-116\end{cases}\left(t\inℤ\right)t\text{ùy}}\text{ý}\)

Ta có: 11x+18y=11(x+y)+9y=120

Do 120 chia 11 dư 10, 11(x+y)\(⋮\)11 => 7y chia 11 dư 10, 9y<120

=> 7y\(\in\){7;14;21;28;35;42;49;56;63;70;77;84;91;98;105;112}

Do 98 chia 11 dư 10 => 7y=98 => y=14

=> 11(x+y)=22 => x+14 = 2 (vô lý)

Do 21 chia 11 dư 10 => 7y=21 => y=3

=> 11(x+y)= 99 => x+3=9 => x=6

Vậy x=6, y=3

Ta thấy 11x chia hết cho 6 nên x chia hết cho 6 . Đặt x = 6k(k nguyên). Thay vào(1) và rút gọn ta được :

         11k + 3y = 20

Biểu thị ẩn mã hệ số của nó có giá trị tuyệt đối nhỏ ( là y ) theo k ta được :

         y = \(\frac{20-11k}{3}\)

 Tách riêng giá trị nguyên của biểu thức này :

         y = 7 – 4k + \(\frac{k-1}{3}\)

Lại đặt \(\frac{k-1}{3}=t\)với t nguyên suy ra k = 3t + 1 . Do đó :

    \(y=7-4\left(3t+1\right)+t=3-11t\)

    x = \(6k=6\left(3t+1\right)=18t+6\)

 Thay các biểu thúc của x và y vào (1) , phương trình được nghiệm đúng .

Vậy các nghiệm nguyên của ( 10 được biểu thị bởi công thức : 

 \(\hept{\begin{cases}\times=18t+6\\y=3-11k\end{cases}}\)Với t là số nguyên tùy ý . 

x=6 ;y=3

trả lời có cả cách giải được k bạn

\(x=\frac{120-18y}{11}=\frac{6\left(20-3y\right)}{11}\)

x nguyên dương =>  20-3y\(\ge\)0 => \(y\le\frac{20}{3}=6,67\) => y=(0,1,2,3,4,5,6) và (120-18y) phải chia hết cho 11

=> 20-3y phải chia hết cho 11 => Chọn được duy nhất y=3

=> x=6

Đáp số: x=6, y=3