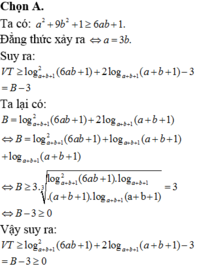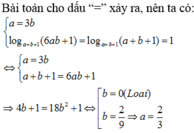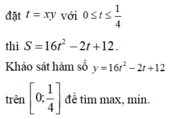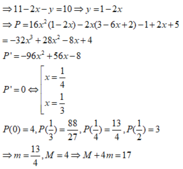Biết thỏa mãn
khi đó giá trị biểu thức
bằng............

Những câu hỏi liên quan
Cho hai số thực dương thỏa mãn a>b.Biết rằng, khi a =a1 và b= b1 thì biểu thức P= a+1/b(a-b) đạt giá trị nhỏ nhất bằng m. Khi đó, giá trị của a1 +b1+m bằng
Xem chi tiết
ta có :
\(P=a+\frac{1}{b\left(a-b\right)}=\left(a-b\right)+b+\frac{1}{b\left(a-b\right)}\ge3\sqrt[3]{\left(a-b\right).b.\frac{1}{b\left(a-b\right)}}=3\)
Vậy m=3
dấu bằng xảy ra khi \(a-b=b=\frac{1}{b\left(a-b\right)}\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}}\)
vậy \(\hept{\begin{cases}a_1=2\\b_1=1\end{cases}\Rightarrow a_1+b_1+m=2+1+3=6}\)
Cho hai số thực x;y thỏa mãn
x
2
+
y
2
≥
9
và
log
x
2
+
y
2
x
8
x
2
+...
Đọc tiếp
Cho hai số thực x;y thỏa mãn x 2 + y 2 ≥ 9 và log x 2 + y 2 x 8 x 2 + 8 y 2 - 7 x - 7 y 2 ≥ 2 . Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=3x+y lần lượt là M và m. Khi đó giá trị của biểu thức M + 2m bằng
![]()
![]()
1 Cho x,y là các số thỏa mãn I x-3 I + (y+4)^2 = 0
2 Số các giá trị nguyên của x thỏa mãn
2(IxI- 5) ( x^2 -9) =0
3 Nếu 1/2 của a bằng 2b thì 9/8a = kb . Vậy kb =
4 Số giá trị của x thỏa mãn
x^2 +7x +12 = 0
5 Biết (a+1) (b+1) = 551 khi đó giá trị của biểu thức ab+a+b = ?
Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
11
−
2
x
−
y
2
y...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Đáp án C
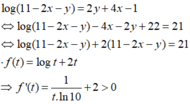
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)
Cho hai số thực a và b thỏa mãn:
log
a
+
b
+
1
2
a
2
+
9
b
2
+
1
+
log
6
a...
Đọc tiếp
Cho hai số thực a và b thỏa mãn: log a + b + 1 2 a 2 + 9 b 2 + 1 + log 6 a b + 1 a + b + 1 2 6 a b + 1 3 = 0 Khi đó giá trị của biểu thức P = 2a + 3b bằng
A. 2
B. 4
C. 5
D. 3
Cho
0
≤
x
,
y
≤
1
thỏa mãn
2017
1
-
x
-
y
x
2
+
2018
y
2...
Đọc tiếp
Cho 0 ≤ x , y ≤ 1 thỏa mãn 2017 1 - x - y = x 2 + 2018 y 2 - 2 y + 2019 . Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = 4 x 2 + 3 y 4 y 2 + 3 x Khi đó M+m bằng bao nhiêu?
A. 383 16
B. 136 3
C. 25 2
D. 391 16
Cho
0
≤
x
,
y
≤
1
thỏa mãn
2017
1
−
x
−
y
x
2
+
2018
y
2
−
2
y
+...
Đọc tiếp
Cho 0 ≤ x , y ≤ 1 thỏa mãn 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 . Gọi M,mlần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y . Khi đó M + m bằng bao nhiêu?
A. 136/3
B. 391/16
C. 383/16
D. 25/2
Đáp án B
Ta có 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 ⇔ 2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018
2017 x x 2 + 2018 = 2017 1 − y 1 − y 2 + 2018 ⇔ f x = f 1 − y
Xét hàm số f t = 2017 t t 2 + 2018 = t 2 .2017 t + 2018.2017 t , có
f ' t = 2 t .2017 t + t 2 .2017 t . ln 2017 + 2018.2017 t . ln 2017 > 0 ; ∀ t > 0
Suy ra f(t) là hàm đồng biến trên 0 ; + ∞ mà f x = f 1 − y ⇒ x + y = 1
Lại có P = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y = 16 x 2 y 2 + 12 x 3 + 12 y 3 + 34 x y
16 x 2 y 2 + 12 x + y 3 − 3 x y x + y + 34 x y = 16 x 2 y 2 + 12 1 − 3 x y + 34 x y = 16 x 2 y 2 − 2 x y + 12
Mà 1 = x + y ≥ 2 x y ⇔ x y ≤ 1 4 nên đặt t = x y ∈ 0 ; 1 4 khi đó P = f t = 16 t 2 − 2 t + 12
Xét hàm số f t = 16 t 2 − 2 y + 12 trên 0 ; 1 4 ta được min 0 ; 1 4 f t = f 1 16 = 191 16 max 0 ; 1 4 f t = f 1 4 = 25 2
Đúng 0
Bình luận (0)
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
và
log
11
-
2
x
-
y
2
y
+
4
x
-
1
. Xét biểu thức
P
16
x...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 và log 11 - 2 x - y = 2 y + 4 x - 1 . Xét biểu thức P = 16 x 2 y - 2 x 3 y + 2 - y + 5 . Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
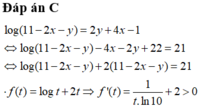
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho x,y,z là các số thực dương thỏa mãn đẳng thức x^2 + y^2 + z^2 + 2xyz = 1. Khi đó giá trị lớn nhất của biểu thức 2x + y + z bằng bao nhiêu?