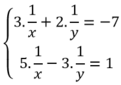Giả sử là nghiệm của phương trình
, ta được
=

Những câu hỏi liên quan
Cho phương trình
A
x
3
+
2
C
x
+
1
x
-
1
-
3
C
x
-
1
x...
Đọc tiếp
Cho phương trình A x 3 + 2 C x + 1 x - 1 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 Giả sử x = x0 là nghiệm của phương trình trên, lúc này ta có
A. x0 ∈(10;13)
B. x0 ∈(12;14)
C. x0 ∈(10;12)
D. x0 ∈(14;16).
Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
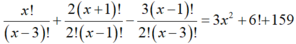
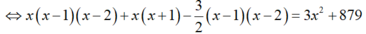
Suy ra x=12.
Chọn B.
Đúng 0
Bình luận (0)
Giả sử các phương trình sau đây đều có nghiệm. Nếu biết các nghiệm của phương trình:
x
2
+
p
x
+
q
0
là lập phương các nghiệm của phương trình
x
2
+
m
x
+
n
0
. Thế thì: A.
p
+
q
m
3
B.
p...
Đọc tiếp
Giả sử các phương trình sau đây đều có nghiệm. Nếu biết các nghiệm của phương trình: x 2 + p x + q = 0 là lập phương các nghiệm của phương trình x 2 + m x + n = 0 . Thế thì:
A. p + q = m 3
B. p = m 3 + 3 m n
C. p = m 3 - 3 m n
D. Một đáp số khác.
Gọi x 1 , x 2 là nghiệm của x 2 + p x + q = 0
Gọi x 3 , x 4 là nghiệm của x 2 + m x + n = 0
- Khi đó, theo vi-et: x 1 + x 2 = - p ; x 3 + x 4 = - m , x 3 . x 4 = n
- Theo yêu cầu ta có:
x 1 = x 3 3 x 2 = x 4 3 ⇒ x 1 + x 2 = x 3 3 + x 4 3 ⇔ x 1 + x 2 = ( x 3 + x 4 ) 3 − 3 x 3 x 4 ( x 3 + x 4 )
⇒ p = - m 3 + 3 m n ⇒ p = m 3 - 3 m n
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Giả sử
x
1
,
x
2
là hai nghiệm của phương trình
x
2
+ px + q 0. Hãy lập một phương trình bậc hai có hai nghiệm
x
1
+
x
2
,
x...
Đọc tiếp
Giả sử x 1 , x 2 là hai nghiệm của phương trình x 2 + px + q = 0. Hãy lập một phương trình bậc hai có hai nghiệm x 1 + x 2 , x 1 x 2
Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0
Đúng 0
Bình luận (0)
Giả sử x là nghiệm của phương trình 4 1 x - 2 = ln e 2 . Tính lnx
A. 0
B. ln3
C. -ln3
D. 1
Để ý rằng
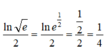
nên phương trình đã cho tương đương với
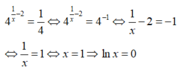
Chọn đáp án A.
Đúng 0
Bình luận (0)
Giả sử x là nghiệm của phương trình 4 l o g 2 x + x 2 = 8 . Tính ( l o g 3 x ) 3
A. 1
B. 8
C. 2 2
D. ± 1
Cho hệ phương trình
4
x
-
3
y
9
2
x
+
...
Đọc tiếp
Cho hệ phương trình 4 x - 3 y = 9 2 x + y = 5
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó x y bằng
A. 12.
B. 12 25
C. 1.
D. 5.
Cho hệ phương trình
2
x
+
y
4
x
+
y
5...
Đọc tiếp
Cho hệ phương trình 2 x + y = 4 x + y = 5
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó x 2 + 2 y bằng
A. 13.
B. 7.
C. 11.
D. 5.
Giả sử a;b là hai nghiệm của phương trình x 2 + mx + 1=0 và b;c là hai nghiệm của phương trình x 2 + nx + 2=0. Chứng minh hệ thức: (b-a)(b-c)=m.n-6.
Vì a, b là 2 nghiệm của phương trình x 2 + mx + 1 = 0 nên theo định lí Vi-et ta có:
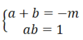
Vì b,c là 2 nghiệm của phương trình x 2 + nx + 2 = 0 nên theo định lí Vi-et ta có:
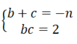
Khi đó:
(b – a)(b – c) = b 2 – bc – ab + ac
= b 2 + bc + ab + ac – 2(ab + bc)
= b( b + c) + a (b + c) – 2 (ab + bc)
= (b + c )( b + a) – 2 (ab + bc)
= (-n).(-m) – 2(1 + 2)
= nm – 6
Đúng 0
Bình luận (0)
Cho hệ phương trình
y
2
-
2
x
+
3
0
5
x
2
-
7
x...
Đọc tiếp
Cho hệ phương trình y 2 - 2 x + 3 = 0 5 x 2 - 7 x y - 6 y 2 = 0 .Giả sử (x;y) là nghiệm của hệ phương trình. Giá trị nhỏ nhất của x 2 + y 2 là:
A. 45
B. 9
C. 2
D. 5
Cho hệ phương trình
3
x
+
2
y
-
7
5
x
-
3...
Đọc tiếp
Cho hệ phương trình 3 x + 2 y = - 7 5 x - 3 y = 1
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó -2x+4y -1 bằng
A. -1
B. -2
C. 0
D. 3