Cho hình cửu giác đều như hình vẽ. Chứng minh rằng BF = BI + BA.
Những câu hỏi liên quan
Cho hình cửu giác đều như hình vẽ. Chứng minh rằng BF = BI + BA.
ai giúp mình tick cho
Bài toán 137
Cho hình cửu giác đều như hình vẽ. Chứng minh rằng BF = BI + BA.
------------------
Các bạn trình bày lời giải đầy đủ của mình vào ô Gửi Ý kiến phía dưới.
Nếu bạn muốn nhờ người ta giải về hình học thì bạn phải cho người ta xem hình rồi mới giải được chứ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
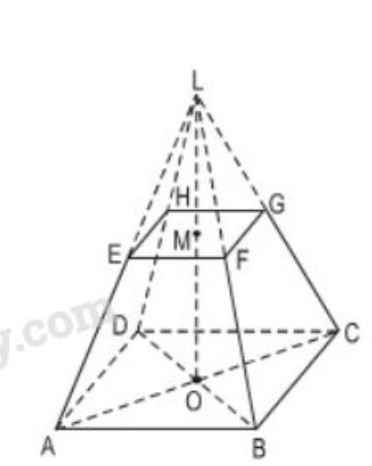
cho hình chóp cụt đều EFGH.DABC, AE, BF, CG, DH cắt nhau tại L như hình vẽ. Chứng minh rằng L.EFGH, L.ABCD là hình chóp đều. Sau đó tính thể tích của hình chọp cụt đều EFGH.DABC
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông như hình 61 là tam giác nhọn ( tức là tam giác có cả ba góc đều là góc nhọn )
Cho hình hộp chữ nhật ABCD.EFGH như hình vẽ.a) Kể tên các đường thẳng được vẽ trên hình và vuông góc vói BF.b) Kể tên ba cặp mặt phẳng vuông góc với nhau.c) AC có vuông góc với DH không? Vì sao?d) Chứng minh tam giác AEG vuông tại E. Từ đó chứng minh
A
G
A
E
2
+
E
F
2
+
E
H...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.EFGH như hình vẽ.
a) Kể tên các đường thẳng được vẽ trên hình và vuông góc vói BF.
b) Kể tên ba cặp mặt phẳng vuông góc với nhau.
c) AC có vuông góc với DH không? Vì sao?
d) Chứng minh tam giác AEG vuông tại E. Từ đó chứng minh A G = A E 2 + E F 2 + E H 2 (AG được gọi là đường chéo hình hộp chữ nhật).
a) Các đường thẳng vuông góc với BF là: AB, BC, CD, DA, AC, EF, FG, GH, HE và FH.
b) (ABCD) và (BCGF), (CDHG) và (EFGH), (ADHE) và (ABCD)
Lưu ý: HS có thể liệt kê tên các cặp mặt phẳng khác.
Đúng 0
Bình luận (0)
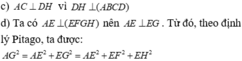
bên trong hình vuông ABCD vẽ tam giác đều ABE. Vẽ tia Bx thuộc nửa mặt phẳng chứa điểm E, có bờ là đường thẳng AB sao cho Bx vuông góc với BE.Trên tia Bx lấy điểm F sao cho BF=BE
a) Tính số đo các góc của tam giác ADE
b) Chứng minh ba điểm D, E, F thẳng hàng
c) Đường tròn tâm O ngoại tiếp tam giác AEB cắt AD tại M. Chứng minh ME//BF
11: Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho
\(\widehat{EDC}=\widehat{ECD}=15^o\)
a) Vẽ điểm F trong hình vuông sao cho \(\widehat{FAD}=\widehat{FDA}=15^o\) . Chứng minh rằng tam
giác DEF là tam giác đều.
b) Chứng minh rằng tam giác ABE là tam giác đều.
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho ∠ (EDC) = ∠ (ECD) = 15 0
Chứng minh rằng tam giác ABE là tam giác đều.
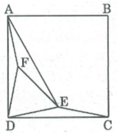
Xét ∆ ADE và ∆ BCE , ta có:
ED = EC (vì AEDC cân tại E)
∠ (ADE) = ∠ (BCE) = 75 0
AD = BC (gt)
Suy ra: ∆ ADE = ∆ BCE (c.g.c)
⇒ AE = BE (1)
* Trong ∆ ADE, ta có:
∠ (AFD) = 180 0 – ( ∠ (FAD) + ∠ (FDA) ) = 180 0 – ( 15 0 + 15 0 ) = 150 0
∠ (AFD) + ∠ (DFE) + ∠ (AFE) = 360 0
⇒ ∠ (AFE) = 360 0 - ( ∠ (AFD) + ∠ (DFE) ) = 360 0 – ( 150 0 + 60 0 ) = 150 0
* Xét ∆ AFD và ∆ AFE, ta có: AF cạnh chung
∠ (AFD) = ∠ (AFE) = 150 0
DE = EF (vì ∆ DFE đều)
Suy ra: ∆ AFD = ∆ AFE (c.g.c) ⇒ AE = AD
Mà AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE
Vậy ∆ AEB đều.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho ∠ (EDC) = ∠ (ECD) = 15 0
Vẽ điểm F trong hình vuông sao cho ∠ (FAD) = ∠ (FDA) = 15 0 . Chứng minh rằng tam giác DEF là tam giác đều.
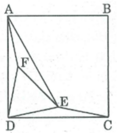
Xét ∆ EDC và ∆ FDA, tacó: ∠ (EDC) = ∠ (FDA) = 15 0
DC = AD (gt)
∠ (ECD) = ∠ (FAD) = 15 0
Suy ra: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Lại có: ∠ (ADC) = ∠ (FDA) + ∠ (FDE) + ∠ (EDC)
⇒ ∠ (FDE) = ∠ (ADC) -( ∠ (FDA) + ∠ (EDC) )= 90 0 - ( 15 0 + 15 0 ) = 60 0
Vậy ∆ DEF đều.
Đúng 0
Bình luận (0)