Tam giác ABC cân tại A cmr : sin A/2 = BC / 2AB

Những câu hỏi liên quan
Cho tam giác ABC cân tại A . CMR Cos B = BC/2AB
Xem chi tiết
ban vẽ hình nhé.
Kẻi AH là đường cao thì AH cũng là đường trung tuyến
Xét tam giác AHB vuông tại H
có cosB = AH/AB = 2AH/2AB = BC/2AB
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. CMR: cosB=\(\dfrac{BC}{2AB}\); và \(\sin\dfrac{A}{2}=\dfrac{BC}{2AB}\)
tam giác ABC cân tại A
Gọi AH là đường cao
=> AH cũng là trung tuyến
=>HB=HC=BC/2=>BC=2HB
ta có cos B = \(\dfrac{BH}{AB}=\dfrac{2BH}{2AB}=\dfrac{BC}{2AB}\) (ĐPCM)
AH là đường cao
=> AH cũng là phân giác
=> góc BAH=CAH=A/2
=> sin \(\dfrac{A}{2}\) =sin BAH =\(\dfrac{BH}{AB}=\dfrac{2BH}{2AB}=\dfrac{BC}{2AB}\)
Đúng 0
Bình luận (2)
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
Bài 1: tính giá trị của đơn thứcB frac{1}{4}left(a^2b^2right)2ab tại a1, b |2|Bài 2 cho tam giác abc vuông cân tại a vẽ AH vuông góc với BC tại H. CMR AB^2+CH^2AC^2+BH^2Bài 3: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt Ac tại M. trên tia BC lấy D sao cho BD BAa) CM tam giác ABM tam giác DBMb) CM MD vuông góc với BCC) Tia BA cắt tia DM tại E. CM AB song song với CE
Đọc tiếp
Bài 1: tính giá trị của đơn thức
B =\(\frac{1}{4}\left(a^2b^2\right)2ab\) tại a=1, b= |2|
Bài 2 cho tam giác abc vuông cân tại a vẽ AH vuông góc với BC tại H. CMR AB^2+CH^2=AC^2+BH^2
Bài 3: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt Ac tại M. trên tia BC lấy D sao cho BD = BA
a) CM tam giác ABM= tam giác DBM
b) CM MD vuông góc với BC
C) Tia BA cắt tia DM tại E. CM AB song song với CE
\(B=\frac{1}{4}\left(a^2b^2\right)2ab\) tại a = 1, b = |2|
\(B=\frac{1}{4}\left(1^2.2^2\right)2.1.2\)
\(B=\frac{1}{4}.4.2.1.2\)
\(B=4\)
Đúng 0
Bình luận (0)
Cho tam giác ABC thỏa mãn BC=2AB và \(\widehat{B}=2\widehat{C}\)
CMR tam giác ABC vuông tại A
1 Cho tam giác ABC cân tại A đường cao AH. M là một điểm bất kì trên cạnh BC. Kẻ đường thẳng qua M và song song với AH cắt AB và AC lần lượt tại N và Qa, CM tam giác ANQ cân b, Tính các góc của tam giác ANQ biết góc ABC70c,Kẻ AI vuông góc với MQ. CM AI song song với BC và AIMH2 Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M trên tia đối của tia CA lấy N sao cho AM+AN2AB. CMR:a, BMCNb,BC cắt MN tại trung điểm I của MN
Đọc tiếp
1 Cho tam giác ABC cân tại A đường cao AH. M là một điểm bất kì trên cạnh BC. Kẻ đường thẳng qua M và song song với AH cắt AB và AC lần lượt tại N và Q
a, CM tam giác ANQ cân
b, Tính các góc của tam giác ANQ biết góc ABC=70
c,Kẻ AI vuông góc với MQ. CM AI song song với BC và AI=MH
2 Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M trên tia đối của tia CA lấy N sao cho AM+AN=2AB. CMR:
a, BM=CN
b,BC cắt MN tại trung điểm I của MN
Cho tam giác ABC cân tại A, H là trung điểm BC, kẻ HE vuông góc AC tại E; HF vuông góc AB tại F
1. CMR tam giác ABH = tam giác ACH
2. CMR tam giác AEF cân
3. CMR EF song song BC
a, xét tam giác ABH và tam giác ACH có AH chung
góc AHC = góc AHB = 90
AB = AC do tam giác ABC cân tại A (gt)
=> tam giác ABH = tam giác ACH (ch-cgv)
b, ta giác ABH = tam giác ACH (câu a)
=> HB = HC (đn)
xét tam giác BHF và tam giác CHE có : góc BFH = góc CEH = 90
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> tam giác BHF = tam giác CHE (ch-gn)
=> BF = CE (đn)
AB = AC (câu a)
BF + FA = AB
CE + AE = AC
=> FA = AE
=> tam giác AFE cân tại A (đn)
c, tam giác AFE cân tại A (Câu b)
=> góc AFE = (180 - góc BAC) : 2 (tc)
tam giác ABC cân tại A (gt) => góc ABC = (180 - góc BAC) : 2 (tc)
=> góc AFE = góc ABC mà 2 góc này đồng vị
=> FE // BC (định lí)
Cho tam giác ABC cân tại A có AB AC 13cm; BC 10cm. Tính sin A A. sin A
120
169
B. sin A
60
169
C. sin A
5
6
D. sin A
10
13
Đọc tiếp
Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A
A. sin A = 120 169
B. sin A = 60 169
C. sin A = 5 6
D. sin A = 10 13
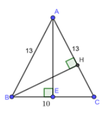
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
![]()
![]()
Mặt khác:
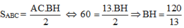
Xét ABH vuông tại H có:
![]()
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
-Cho tam giác ABC vuông tại A , có BC=2AB . Gọi H là trung điểm của BC , đường thẳng vuông góc với BC tại H cắt AC tại M.
a) Biết ABC = 60 độ , tính góc C ?
b) Chứng minh tam giác MAB = tam giác MHB.
c) Chứng minh tam giác MBC cân
d) Chứng minh BM là đường trung trực của AH
giúp với ạ cần hình gấp😭














