Cho hình thoi ABCD có O là giao điểm 2 đường chéo,I là trung điểm BC,E đối xứng với O qua I
a)Cm OCEB là hcn
b)Cm DOEC là hbh
c)F là giao điểm của AE và BC.Tính FB/FC
Những câu hỏi liên quan
Cho hình thoi ABCD có O là giao điểm 2 đường chéo,I là trung điểm BC,E đối xứng với O qua I
a)Cm OCEB là hcn
b)Cm DOEC là hbh
c)F là giao điểm của AE và BC.Tính FB/FC
mình chẳng về được cái hình nữa
Đúng 0
Bình luận (0)
a, Xet tu giac OCEB co :
I la trung diem cua BC (IB=IC)
I là trung điểm của OE (IO=IE)
=> OCEB la hbh
Ma AC vuong voi BD
Hay AO vuong voi OB
=> goc O=90
Ma trong hinh binh hanh co 1 goc vuong la hinh chu nhat
=> OCEB la HCN
b, Xet tu giac DOEC co :
OB=OD
Ma : OB=CE (t/c HCN)
=> OD=CE
Va : OB//CE=>OD//CE
Vay ODCE là hình bình hành .
c, k pt
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là điểm đối xứng với O qua I.
b) Chứng tỏ E đối xứng với A qua trung điểm J của đoạn OB.
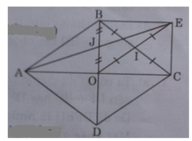
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
Đúng 0
Bình luận (0)
Cho hình thoi ABCD, có O là giao điểm của 2 đường chéo. Gọi I là trung điểm BC, E là điểm đối xứng với O qua I
a, tứ giác OBEC là hình gì
b, Chứng tỏ E đối xứng với A qua I
Cho hình bình hành ABCD. Gọi O là giao điểm ha đường chéo. Lấy E trên AB , F trên CD sao cho AE = CF
a) Chứng minh E đối xứng với F qua O
b) Gọi I là gio của AF và DEsao cho AE = CF, K là giao của BF và CE. CM I đối xứng với K qua O
cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo. Gọi M,N là trung điểm của OB,OD.
a)cm: AMCN là hình bình hành
b)AN cắt CD tại E, CM cắt AB tại F
cm: AE=CF và O,E,F thẳng hàng
c)cm: E đối xứng vói F qua O
mọi người giúp em với ạ.
a: Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó: AMCN là hình bình hành
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có O là giao điểm hai đường chéo AC và BD. Gọi I là trung điểm BC, E đối xứng với O qua I.1.Chứng minh rằng: OE DA2.Chứng minh rằng: E đối xứng với A qua trung điểm J của đoạn OB3.Chứng minh rằng: SABCD 2SBOCE.4.M đối xứng với I qua J. Chứng minh rằng: ba điểm A, M, B thẳng hàng.5.Gọi K là giao điểm AI và BO. Chứng minh rằng: Ba điểm M, K, C thẳng hàng
Đọc tiếp
Cho hình thoi ABCD có O là giao điểm hai đường chéo AC và BD. Gọi I là trung điểm BC, E đối xứng với O qua I.
1.Chứng minh rằng: OE = DA
2.Chứng minh rằng: E đối xứng với A qua trung điểm J của đoạn OB
3.Chứng minh rằng: SABCD = 2SBOCE.
4.M đối xứng với I qua J. Chứng minh rằng: ba điểm A, M, B thẳng hàng.
5.Gọi K là giao điểm AI và BO. Chứng minh rằng: Ba điểm M, K, C thẳng hàng
1: OI=CD/2
=>OE=CD
hay OE=AD
Đúng 0
Bình luận (0)
1.cho hbh ABCD có hai đường chéo AC và BD cắt nhau tại O . gọi E là điểm bất kì trên cạnh AB , tia EO cắt DC tại F . Cm: E và F đối xứng nhau qua O2. cho tam giác ABC cân tại A và D là điểm đối xứng của A qua BC .a.gọi F là giao điểm của AD và AC . tứ giác ABDC là hình gì ? vì sao?b. gội E là điểm đối xứng với C qua A . cm: EB vuông vơi BCc. tứ giác ADBE là hình gì vì saod. đường thẳng È cắt AB tại G . CM: GA1/2 GBe. đường thẳng CG cắt AF tại I CM: IAIF
Đọc tiếp
1.cho hbh ABCD có hai đường chéo AC và BD cắt nhau tại O . gọi E là điểm bất kì trên cạnh AB , tia EO cắt DC tại F . Cm:
E và F đối xứng nhau qua O
2. cho tam giác ABC cân tại A và D là điểm đối xứng của A qua BC .
a.gọi F là giao điểm của AD và AC . tứ giác ABDC là hình gì ? vì sao?
b. gội E là điểm đối xứng với C qua A . cm: EB vuông vơi BC
c. tứ giác ADBE là hình gì vì sao
d. đường thẳng È cắt AB tại G . CM: GA=1/2 GB
e. đường thẳng CG cắt AF tại I CM: IA=IF
hình bình hành ABCD. O là giao điểm của 2 đường chéo. Gọi M,N thứ tự là trung điểm của OD và OB. Gọi E là giao điểm của AM và DC, F là giao điểm của CN và AB
a,Cm tứ giác AMCN và AECF là hình bình hành
b, Cm E, F đối xứng với nhau qua O
c,Cm DE=1/2.EC
cho hình bình hành ABCD, BCH = 2AB , E , Ford lần lượt là trung điểm BC và DA .
a) cm :BEDF là hình bình hành
b) cm : ABEF là hình thoi và AC , BD , EF đồng quy
c) cho i là điểm đối xứng A qua B. cm : i đối xứng D qua AE
d) cho P là giao điểm của AE và DF
Q là giao điểm của FC và DE. Tìm điều kiện ABCD để PEQF là hình vuông.
cm là chứng mình nha