cho hàm số y = f(x) = 2 - x2−2x+1−−−−−−−−−−√x2−2x+1
a) vẽ ddooof thị hàm số trên
b) tìm tất cả các giá trị của x sao cho f(x)≤≤1
cho hàm số y = f(x) = 2 - \(\sqrt{x^2-2x+1}\)
a) vẽ ddooof thị hàm số trên
b) tìm tất cả các giá trị của x sao cho f(x)\(\le\)1
tìm tất cả các giá trị của m sao cho đồ thị hàm số cắt đồ thị hàm số tại \(y=x^2+2mx+4\) đúng 2 điểm phân biệt có hoành độ thỏa mãn
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số y = f(x) = x 4 - 2 ( m - 1 ) x 2 + 1 . Tìm tất cả các giá trị của tham số m để đồ thị hàm số có 3 điểm cực trị lập thành một tam giác vuông.
A. m = -1.
B. m = 0.
C. m = 1.
D. m = 2.
Chọn D.
![]() TXĐ: D = R.
TXĐ: D = R.
![]()
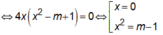
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt ⇔ m -1 > 0 ⇔ m > 1(*)
3 điểm cực trị của đồ thị hàm số là: A(0;1),
Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
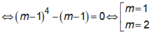
Kết hợp với điều kiện (*) => m = 2
Làm theo bào toán trắc nghiệm như sau:
Hàm số đã cho có 3 điểm cực trị khi ab < 0 ![]()
Chỉ có đáp án D thỏa mãn.
cho hàm số y=-2x+1a)Xác định tọa độ giao điểm của đồ thị hàm số trên và Ox,Oy
b)CMR:f(x1)+f(x2)=f(x1+x2)+1
c)Tìm tọa độ giao điểm của đồ thị hàm số trên và đồ thị hàm số y=|x|
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
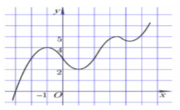
Cho hàm số y = f(x) có đồ thị hàm số như hình vẽ dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f( x 2 - 2 x ) trên đoạn [ - 3 2 ; 7 2 ] Tìm khẳng định đúng trong các khẳng định sau
A. ![]()
B.![]()
C.![]()
D.![]()
Cho hàm số y = f(x) có đồ thị hàm số như hình vẽ dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f ( x 2 - 2 x ) trên đoạn - 3 2 ; 7 2 . Tìm khẳng định sai trong các khẳng định sau.
![]()
![]()
![]()
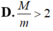
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số f(x) có đồ thị của hàm số y=f’(x) như hình vẽ:
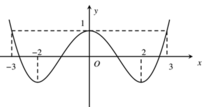
Hàm số y = f ( 2 x - 1 ) + x 3 3 + x 2 - 2 x nghịch biến trên khoảng nào sau đây
A. (-1;0).
B. (-6;-3).
C. (3;6).
D. (6;+∞).
Cho hàm số y = f ( x ) = x 3 - ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tất cả các giá trị của tham số m để hàm số y=f(|x|) có 5 điểm cực trị
A. 5 4 < m ≤ 2
B. - 2 < m < 5 4
C. - 5 4 < m < 2
D. 5 4 < m < 2