Cho 100 điểm A1,A2,...A99,A100; trong đó không có ba điểm nào thẳng hàng. Kẻ các đường thẳng đi qua hai điểm.Hỏi có bao nhiêu đường thẳng.

Những câu hỏi liên quan
Khai triển
x
-
3
100
ta được đa thức
x
-
3
100
a
0
+
a
1
x
+
a
2
x
2
+
.
.
....
Đọc tiếp
Khai triển x - 3 100 ta được đa thức x - 3 100 = a 0 + a 1 x + a 2 x 2 + . . . + a 100 x 100 với a 0 , a 1 , a 2 , . . . , a 100 là các hệ số thực. Tính a 0 - a 1 + a 2 - . . . - a 99 + a 100
A. - 2 100
B. 4 100
C. - 4 100
D. 2 100
Cho a1-1/100=a2-2/99=a3-3/98=...=a100-100/1
Và a1+a2+a3+...+a100=10100
Tính a1,a2,a3,...,a100
Xem chi tiết
Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
\(\frac{a_1-1}{100}=\frac{a_2-2}{99}=...=\frac{a_{100}-100}{1}=\frac{a_1+a_2+...+a_{100}-5050}{5050}=\frac{10100-5050}{5050}=\frac{5050}{5050}=1\)
\(\Rightarrow a_1-1=100\)
\(a_2-2=99\)
...
\(a_{100}-100=1\)
\(\Rightarrow a_1=a_2=...=a_{100}=101\)
Khai triển
x
-
3
100
ta được đa thức
x
-
3
100
a
0
+
a
1
x
+
a
2
x
2
+...
Đọc tiếp
Khai triển x - 3 100 ta được đa thức x - 3 100 = a 0 + a 1 x + a 2 x 2 + . . . + a 100 x 100 với a 0 a 1 a 2 . . . a 100 là các hệ số thực. Tính a 0 - a 1 + a 2 - . . . - a 99 + a 100 ?
A. - 2 100
B. 4 100
C. - 4 100
D. 2 100
tìm các số a1 a2 ... a100 biết:
a1-1/100=a2-2/99=...=a100-100/1 và a1+a2+...+a100=10100
Câu hỏi của Ngọc Ánh - Toán lớp 10 | Học trực tuyến
Bạn tham khảo link tại đây nhé
Đúng 0
Bình luận (0)
Em tham khảo link này nhé! Câu hỏi của Ngọc - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
a,cho a1 +a2+a3+.....+a101=0 và a1 +a2= a3+a4=.....=a99+a100=-1
Tìm a101
b,tìm số nguyên a biết
-2017</a+4/< hoặc = 2
a.
Theo đề bài ta có:
-1 - 1 - ... - 1 + a101 = 0
=> - 50 + a101 = 0=> a101 = 50
b,
-2017 < |a+4| ≤ 2
=> 0 ≤ |a+4| ≤ 2
=> -2 ≤ a+4 ≤ 2
=> -6 ≤ a ≤ -2
Đúng 0
Bình luận (0)
Tìm a1;a2;a3;...a100
biết (a1-1)/100=(a2-2)/99=...=(a100-100)/1
và a1+a2+a3+...+a100=10100
mình xin lỗi nhung mình ko biết viết chữ a1 (số 1 ở phía dưới chữ a) các chữ a2; a3 ..a100 cũng vậy nha
Câu 1:
cho 100 số nguyên dương a1, a2,... a100 thỏa mãn:
\(\frac{1}{a1^2}+\frac{1}{a2^2}+...+\frac{1}{a100^2}=\frac{199}{100}\)
chứng minh: trong 100 số a1, a2,... a100 đã cho tồn tại ít nhất 2 số bằng nhau.
Giả sử trong 100 số nguyên dương đã cho không tồn tại 2 số nào bằng nhau
Không mất tính tổng quát, giả sử \(a_1< a_2< a_3< ...< a_{100}\)
\(\Rightarrow a_1\ge1;a_2\ge2;a_3\ge3;....;a_{100}\ge100\Rightarrow\frac{1}{a_1^2}+\frac{1}{a_2^2}+\frac{1}{a^2_3}...+\frac{1}{a^2_{100}}\le\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}\left(1\right)\)
Lại có: \(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=\frac{199}{100}\left(2\right)\)
Từ (1) và (2) => \(\frac{1}{a_1^2}+\frac{1}{a^2_2}+...+\frac{1}{a^2_{100}}< \frac{199}{100}\) trái với giả thiết
Vậy tồn tại ít nhất 2 số bằng nhau trong 100 số a1,a2,...,a100
Đúng 0
Bình luận (0)
tính a1, a2,...a100
biết \(\frac{a1-1}{100}=\frac{a2-2}{99}=...=\frac{a100-100}{1}\)
và a1+a2+...+a100=10100
http://olm.vn/hoi-dap/question/133393.html
bạn xem ở đây nhé
Đúng 0
Bình luận (0)
http://olm.vn/hoi-dap/question/133393.html
Bạn bấm theo là có mà xem
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho 100 so tu nhien tu a1;a2;a3;...;a100
1/a1 +1/a2+....+1/a100=101/2
cmr it nhat 2 trong 100 so tu nhien tren bang nhau




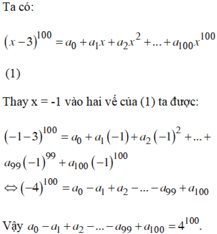

![Yuri Sweet[𝕿𝖊𝖆𝖒 𝕹𝖊𝖕𝖆𝖑]](https://hoc24.vn/images/avt/avt6428199_256by256.jpg)















