Tìm cặp số nguyên (x, y) biết : x(y + 2) = y + 5

Những câu hỏi liên quan
Tìm cặp số nguyên (x;y) biết: x(y+2) = y+5
BÀi 1:Tìm các cặp số nguyên x,y biết 2x2+y2+xy=2(x+y)
Bài 2:Tìm các cặp số nguyên dương x,y biết x2+y2=3(x+y)
Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
Đúng 0
Bình luận (0)
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)
Đúng 0
Bình luận (0)
tìm các cặp số nguyên x,y biết:
|x-2| - |y-5| = 2
Đối với dạng toán này theo mình,ta cần tìm nghiệm tổng quát chứ không phải nghiệm riêng lẻ.
Từ đề bài suy ra: | x - 2 | - | y - 5 | - 2 = 0 (1)
+)Xét \(x-2\ge0;y-5\ge0\Leftrightarrow x\ge2;y\ge5\)
(1) trở thành: \(x-2-y+5-2=0\Leftrightarrow\left(x-y\right)-\left(2-5+2\right)=0\)
\(\Leftrightarrow x-y+1=0\Leftrightarrow x=y-1\) (đk \(x\ge2;y\ge5\))
+)Xét x - 2 < 0; y -5 < 0 tức là x < 2;y<5
Khi đó vế trái sẽ < 2 (vô lí)
vậy \(\hept{\begin{cases}x=y-1\\y\ge5\left(y\inℤ\right)\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1 tìm các cặp số nguyên x;y biết
a. ( x-2).(y-3)=5
b. (1-x)(y+1)=3
Do x, y nguyên
nên : x-2 và y-3 cũng đạt giá trị nguyên
Ta có : 5 = 1.5 = (-1).(-5)
Bảng giá trị :
| x-2 | 1 | 5 | -1 | -5 |
| y-3 | 5 | 1 | -5 | -1 |
| x | 3 | 7 | 1 | -3 |
| y | 8 | 4 | -2 | 2 |
Vậy (x;y)=(3;8);(7;4);(1;-2);(-3;2)
Đúng 2
Bình luận (0)
Do x, y nguyên
Nên 1-x và y+1 cũng đạt giá trị nguyên
Ta có : 3=1.3=(-1).(-3)
Bảng giá trị :
| 1-x | 1 | 3 | -1 | -3 |
| y+1 | 3 | 1 | -3 | -1 |
| x | 0 | -2 | 2 | 4 |
| y | 2 | 0 | -4 | -2 |
Vậy (x;y)=(0;2);(-2;0);(2;-4);(4;-2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm các cặp số nguyên x,y biết x/5-1/y+2=1/10
a) Tìm cặp số nguyên (x;y) để B = 1/x-y : x+2 / 2(x-y) là số nguyên.
b) Tìm x biết: |x(x^2 - 5/4)| = x.
\(\left|x\left(x^2-\frac{5}{4}\right)\right|=x\)
\(\Leftrightarrow\hept{\begin{cases}x\left(x^2-\frac{5}{4}\right)=x\\x\left(x^2-\frac{5}{4}\right)=-x\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2-\frac{5}{4}=\frac{x}{x}\\x^2-\frac{5}{4}=-\frac{x}{x}\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2-\frac{5}{4}=1\\x^2-\frac{5}{4}=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2=\frac{9}{4}\\x^2=\frac{1}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\pm\frac{3}{2}\\x=\pm\frac{1}{2}\end{cases}}\)
vậy ....
\(\left|x\left(x^2-\frac{5}{4}\right)\right|=x\Leftrightarrow\left|x^3-\frac{5}{4}x\right|=x\)
\(\Leftrightarrow\hept{\begin{cases}x^3-\frac{5}{4}x=x\\x^3-\frac{5}{4}x=-x\end{cases}\Leftrightarrow\hept{\begin{cases}x\left(x^2-\frac{5}{4}\right)=x\\x\left(x^2-\frac{5}{4}\right)=-x\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2-\frac{5}{4}=\frac{x}{x}\\x^2-\frac{5}{4}=-\frac{x}{x}\end{cases}\Leftrightarrow\hept{\begin{cases}x^2-\frac{5}{4}=1\\x^2-\frac{5}{4}=-1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2=\frac{9}{4}\\x^2=\frac{1}{4}\end{cases}\Leftrightarrow\hept{\begin{cases}x=\pm\frac{3}{2}\\x=\pm\frac{1}{2}\end{cases}}}\)
Tìm cặp số nguyên x,y biết
a, x/y = 2/5
b, x/3=y/7
Tìm các cặp số nguyên x, y biết x + y = 5
Tìm các cặp số nguyên x,y biết:
x/2=-1/y
x/-3=1/y
x/5=1/y
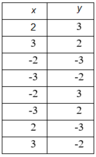
\(\frac{x}{2}=\frac{-1}{y}\Rightarrow xy=-2\Rightarrow x;y\inƯ\left(-2\right)=\left\{\pm1;\pm2\right\}\)
| x | 1 | -1 | 2 | -2 |
| y | -2 | 2 | -1 | 1 |
\(\frac{x}{-3}=\frac{1}{y}\Rightarrow xy=-3\Rightarrow x;y\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x | 1 | -1 | 3 | -3 |
| y | -3 | 3 | -1 | 1 |
tương tự 2 phần dưới