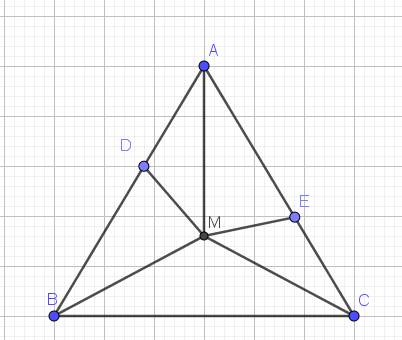
Cho tam giác ABC cân tại A, lấy M trên cạnh BC, qua M vẽ các đường // với AB và AC lần lượt cắt AC và AB tại D,E. C/m ME=AE và ME=AD suy ra MD+ME=AB=AC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A,lấy M trên cạnh BC qua M vẽ các đường // với AB và AC lần lượt cắt AC vàAB tại D,E
a) C/m các tam giác CMD và BME là các tam giác cân
b)C/m MD=AE và ME=AD suy ra MD+ME=AB
cho tam giác ABC cân tại A,lấy M trên cạnh BC,qua M vẽ các đường // với AB và AC lần lượt cắt AC và AB tại D,E.C/m:ME=AD suy ra MD+ME=AB=AC
cho tam giác ABC cân tại A,lấy M trên cạnh BC,qua M vẽ các đường // với AB và AC lần lượt cắt AC và AB tại D,E.C/m:ME=AD suy ra MD+ME=AB=AC
các bạn nhớ trình bày luôn nhé bạn nào nhanh và đúng mình cho ****
Đùa hả ? Câu hỏi toán thì OLM xóa làm gì
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A,lấy M trên cạnh BC,qua M vẽ các đường // với AB và AC lần lượt cắt AC và AB tại D,E.C/m:ME=AD suy ra MD+ME=AB=AC
các bạn nhớ trình bày luôn nhé bạn nào nhanh và đúng mình cho ****
và online math đừng xóa
xét tứ giác AEDM, ta có:
AE // DM (AB // DM, E thuộc AB)
EM // AD (EM // AC, D thuộc AC)
=> tứ giác AEDM là hình bình hành
=> EA = DM ; EM = AD (đpcm)
có DM // AB (giả thiết) => góc DMC=ABM (đồng vị) (1)
mà ABM=ACB (tam giác ABC cân tại A) (2)
từ (1) và (2) suy ra tam giác MDC cân tại D
=> DC=DM
mà DC+AD = AC
=> MD + ME = AC =AB
Đúng 0
Bình luận (0)
3) Cho tam giác ABC cân tại A, lấy M trên tia đối của tia BC. Qua M vẽ các đường thẳng thẳng góc với AB và AC cắt AC và AB tại D,E . C/m MD - ME không đổi khi M chạy trên cạnh BC
Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E. Cm: ME=AD và MD=AE
Xét tứ giác AEMD có : MD // AE (vì MD // AB) và ME // AD (vì ME // AC)
=> AEMD là hình bình hành. Theo tính chất của hình bình hánh ta suy ra được ME = AD và MD = AE (đpcm).
Đúng 0
Bình luận (0)
Cho góc xoy=90°, điểm M nằm trong góc đó . Vẽ điểm A và B sao cho Ox là đường trung trực của MA, Oy là đường trung trực của MB . CM OA=OB
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A Hai đường trung trực của BC và AB cắt nhau tại M trên cạnh AB lấy điểm D và trên cạnh AC lấy điểm E sao cho AD=CE CMR
MD=ME
Lời giải:
Vì $M$ nằm trên trung trực của $BC$ nên $MB=MC$. $M$ nằm trên đường trung trực của $AB$ nên $MA=MB$
$\Rightarrow MA=MB=MC$
Xét tam giác $AMC$ và $AMB$ có:
$AM$ chung
$AC=AB$ (do $ABC$ là tam giác cân tại $A$)
$MB=MC$
$\Rightarrow \triangle AMC=\triangle AMB$ (c.c.c)
$\Rightarrow \widehat{ACM}=\widehat{ABM}$
Hay $\widehat{ECM}=\widehat{ABM}$
Mà $\widehat{ABM}=\widehat{MAB}$ (do tam giác $MAB$ cân tại $M$ vì $MA=MB$)
$\Rightarrow \widehat{ECM}=\widehat{MAB}=\widehat{DAM}$
Xét tam giác $ECM$ và $DAM$ có:
$EC=DA$ (gt)
$\widehat{ECM}=\widehat{DAM}$ (cmt)
$CM=AM$ (cmt)
$\Rightarrow \triangle ECM=\triangle DAM$ (c.g.c)
$\Rightarrow ME=MD$ (đpcm)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A ,hai đường trung trực của AB và AC cắt nhau tại M .Trên cạnh AB lấy điểm D và trên cạnh AC lấy điểm E sao cho AD =CE.
a,chứng minh MD=ME
b,Khi D di chuyển trên cạnh AB và AC sao cho AD =CE thì các đường trung trực của DE luôn đi qua 1 điểm cố định M
cho tam giác ABC cân tại A lấy M trên tia đối của tia BC.Từ M vẽ các đường thẳng thẳng góc với AB và AC cắt AB,AC tại D và E.C/m MD+ME không đổi khi M chạy trên cạnh BC.(gợi ý BH thẳng góc AC tại H,vẽ MI thẳng góc BH tại I)