Các bn giúp mk làm bài 67 của phần số thập phân hữu hạn và số thập phân vô hạn tuần hoàn đc ko

Những câu hỏi liên quan
Chọn câu đúng
Số 2,4444... là:
A. Số thập phân hữu hạn
B. Số thập phân vô hạn tuần hoàn có chu kì là 2
C. Số thập phân vô hạn tuần hoàn có chu kìa là 4
D. Số thập phân vô hạn tuần hoàn có chu kì là 24
ai giúp mik với mik cần gấp ạ
Xem thêm câu trả lời
Cách so sánh số thập phân vô hạn tuần hoàn và số thập phân vô hạn ko tuần hoàn???
Để so sánh số thập phân vô hạn tuần hoàn và số thập phân vô hạn không tuần hoàn, ta cần hiểu rõ đặc điểm của từng loại số, rồi từ đó đưa ra phương pháp so sánh phù hợp.
🌟 1. Định nghĩa nhanh:Số thập phân vô hạn tuần hoàn: Là số thập phân có một dãy chữ số lặp lại mãi mãi sau dấu phẩy.Ví dụ:\(0.6666 \ldots = 0. \overset{\overline}{6}\)\(1.272727 \ldots = 1.27 \overset{\overline}{27}\)Số thập phân vô hạn không tuần hoàn: Là số thập phân không có phần lặp lại, tức là các chữ số sau dấu phẩy không theo quy luật nào và kéo dài vô hạn. Đây là đặc điểm của các số vô tỉ.
Ví dụ:\(\pi = 3.14159265 \ldots\)\(\sqrt{2} = 1.4142135 \ldots\)🧠 2. Cách so sánh✳️ Trường hợp 1: So sánh bằng giá trị gần đúngCắt các số đến cùng một số chữ số thập phân (ví dụ đến 10 chữ số sau dấu phẩy).So sánh 2 số tại từng chữ số như khi so sánh số tự nhiên.Nếu cần độ chính xác cao → tiếp tục lấy thêm chữ số.
Cách này dùng được cho mọi loại số, nhưng là phương pháp gần đúng, thích hợp khi không cần tuyệt đối chính xác (ví dụ trong tính toán ước lượng).
✳️ Trường hợp 2: Dùng dạng phân số (chỉ áp dụng cho số tuần hoàn)Số thập phân vô hạn tuần hoàn luôn có thể chuyển về phân số hữu tỉ.Ví dụ:\(0. \overset{\overline}{3} = \frac{1}{3}\),
\(1.2 \overset{\overline}{7} = \frac{124}{99}\)Số thập phân vô hạn không tuần hoàn là số vô tỉ, không thể viết dưới dạng phân số.
➡️ Từ đây có thể thấy:
Một số thập phân vô hạn tuần hoàn luôn nhỏ hơn, lớn hơn hoặc bằng một số thập phân vô hạn không tuần hoàn tùy theo giá trị thực tế.
📌 Ví dụ so sánh cụ thể:
So sánh \(0. \overset{\overline}{6}\) và \(\sqrt{2} - 1\)\(0. \overset{\overline}{6} = \frac{2}{3} \approx 0.666666 \ldots\)\(\sqrt{2} \approx 1.4142135 \ldots \Rightarrow \sqrt{2} - 1 \approx 0.4142135 \ldots\)➡️ \(0. \overset{\overline}{6} > \sqrt{2} - 1\)
✅ Tóm lại: Cách so sánhLoại so sánh | Cách làm |
|---|---|
So sánh gần đúng | Lấy giá trị gần đúng đến nhiều chữ số thập phân, rồi so sánh |
So sánh chính xác | Nếu số tuần hoàn → chuyển về phân số; nếu số còn lại là số vô tỉ → dùng giá trị gần đúng hoặc lý luận bất đẳng thức |
Tham khảo
Đúng 0
Bình luận (0)
Để so sánh số thập phân vô hạn tuần hoàn và số thập phân vô hạn tuần hoàn, bạn cần chế độ xem xác định có một chuỗi số lặp lại vô hạn sau comma hay không. Nếu có một dãy số được lặp lại thì đó là số thập phân vô hạn tuần. Ngược lại, nếu các chữ số sau comma kéo dài mãi mãi nhưng không bao giờ lặp lại theo một quy tắc nhất định, thì đó là số thập phân vô hạn không tuần hoàn.
Đúng 0
Bình luận (0)
a) Trong các phân số sau đây , phân số nào viết được dưới dạng số thập phân hữu hạn , phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn .Giair thích.frac{5}{8};frac{-3}{20};frac{4}{11};frac{15}{22};frac{-7}{12};frac{14}{35}b) Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn (viết gọn với chu kì trong dấu ngoặc)GIÚP MK VS , MK ĐANG CẦN GẤP
Đọc tiếp
a) Trong các phân số sau đây , phân số nào viết được dưới dạng số thập phân hữu hạn , phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn .Giair thích.
\(\frac{5}{8};\frac{-3}{20};\frac{4}{11};\frac{15}{22};\frac{-7}{12};\frac{14}{35}\)
b) Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn (viết gọn với chu kì trong dấu ngoặc)
GIÚP MK VS , MK ĐANG CẦN GẤP![]()
a)
– Phân số \(\frac{5}{8}\) được viết dưới dạng số thập phân hữu hạn vì có mẫu 8 = 23 không có ước nguyên tố khác 2 và 5
– Phân số \(-\frac{3}{20}\) được viết dưới dạng số thập phân hữu hạn vì có mẫu 20 = 22 . 5 không có ước nguyên tố khác 2 và 5
– Phân số \(\frac{14}{35}\) được viết dưới dạng số thập phân hữu hạn vì \(\frac{14}{35}\) = 2/5, mẫu 5 không có ước nguyên tố khác 2 và 5
– Các phân số \(\frac{4}{11}\); \(\frac{15}{22}\); 7/12 có mẫu lần lượt là 11 = 1 . 11; 22 = 2 . 11; 12 = 3 . 22 đều chứa ước nguyên tố khác 2 và 5 nên được viết dưới dạng số thập phân vô hạn tuần hoàn.
b) 5/8 = 0,625; −3/20 = -0,15; 14/35 = 2/5 = 0,4
4/11 = 0,(36); 15/22 = 0,6(81); 7/12 = 0,58(3)
Đúng 0
Bình luận (3)
phân số 61/110 là:
A.số thập phân hữu hạn
B.số thập phân vô hạn tuần hoàn
C.số thập phân vô hạn không tuần hoàn
phân số 61/110 là:
A.số thập phân hữu hạn
B.số thập phân vô hạn tuần hoàn
C.số thập phân vô hạn không tuần hoàn
k cho mk nha
phân số 61/110 là:
A.số thập phân hữu hạn
B.số thập phân vô hạn tuần hoàn
C.số thập phân vô hạn không tuần hoàn
Sau khi viết được dưới dạng số thập phân, ta được số thập phân hữu hạn hay vô hạn tuần hoàn đơn hay vô hạn tuần hoàn tạp.
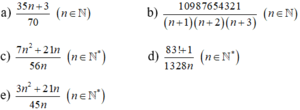
a) 35 n + 3 70 = 35 n + 3 2.5.7 n ∈ ℕ vì mẫu chứa thừa số nguyên tố 7, 2 và 5 mà tử không chia hết cho 7 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
b) 10987654321 n + 1 n + 2 n + 3 n ∈ ℕ có mẫu là ba số tự nhiên liên tiếp nên mẫu chứa các thừa số nguyên tố 2 và 3. Mà tử không chia hết cho 3, 2 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
c) 7 n 2 + 21 n 56 n = 7 n n + 3 7 n .8 = n + 3 2 3 n ∈ ℕ * phân số viết được dưới dạng số thập phân hữu hạn.
d) 83 ! + 1 1328 n n ∈ ℕ *
Vì tử số là 83 ! + 1 không chia hết cho 83, mẫu 1328 n = 83.16 n ⋮ 83 n ∈ N * nên khi phân số là phân số tối giản thì mẫu vẫn chứa ước nguyên tố là 83. Lại có tử không chia hết cho 2, mẫu chia hết cho 2 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
e) 3 n 2 + 21 n 45 n = 3 n n + 7 3 n .15 = n + 7 3.5 n ∈ ℕ *
· Nếu lại có n chia 5 dư 3 thì phân số viết được dưới dạng số thập phân vô hạn tuần hoàn đơn.
· Nếu n chia 5 có số dư khác 3 thì phân số viết được dưới dạng số thập phân vô hạn tuần hoàn tạp.
Đúng 1
Bình luận (0)
Trong các khẳng sau, khẳng định nào sai?A. Mỗi số thạp phân vô hạn tuần hoàn đều là số hữa tỉ.B. Mỗi số thập phân hữu hạn đều là một số hữu tỉ.C. Mỗi số hữu tỉ đều được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoànD. Một phân số có mẫu dương mà mẫu có ước nguyên tố khác và thì phân số đó được viết dưới dạng số thập phân hữu hạn.
Đọc tiếp
Trong các khẳng sau, khẳng định nào sai?
A. Mỗi số thạp phân vô hạn tuần hoàn đều là số hữa tỉ.
B. Mỗi số thập phân hữu hạn đều là một số hữu tỉ.
C. Mỗi số hữu tỉ đều được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn
D. Một phân số có mẫu dương mà mẫu có ước nguyên tố khác và thì phân số đó được viết dưới dạng số thập phân hữu hạn.
Một phân số có mẫu dương mà mẫu có ước nguyên tố khác gì và gì thì phân số đó được viết dưới dạng số thập phân hữu hạn hả bạn
Đúng 1
Bình luận (0)
D
Nghĩ là z (vì bn ghi ko rõ nên mik ko hiểu) tại mấy câu kia đúng
Đúng 1
Bình luận (0)
a, Trong các phân số sau đây , phân số nào viết được dưới dạng số thập phân hữu hạn , phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn ? giải thích .
5/8 ; -3/20 ; 4/11 ; 15/22 ; -7/12 ; 14/35
b , Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn ( viết gọn với chu kì trong dấu ngoặc )
Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)
Sách bài tập toán. Bài 9 số thập phân hữu hạn. Số thập phân vô hạn tuần hoàN
Cho mik đề
Đề bài
Bài 1: Viết phân số sau dưới dạng số thập phân hữu hạn: −3/8 ; 21/20
Bài 2: Viết số thập phân hữu hạn thành dạng phân số: 0,15; 1,32.
Bài 3: Vì sao số 2/3 viết được dưới dạng số thập phân vô hạn tuần hoàn?
Hãy viết số thập phân vô hạn tuần hoàn đó.
Bài 4: Viết số thập phân vô hạn tuần hoàn sau thành phân số:
0,(15)
Bài 5: Thực hiện các phép tính:
a) 0,(3)+0,(7)0,(3)+0,(7)
b) 0,(12)−0,(3).
Đúng 0
Bình luận (0)
Trả lời câu hỏi Toán 7 Tập 1 Bài 9 trang 33: Trong các phân số sau đây phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? Viết dạng thập phân của các phân số đó.
![]()
Bài 65 (trang 34 SGK Toán 7 Tập 1): Giải thích vì sao các phân số sau viết dưới dạng số thập phân hữu hạn rồi viết chúng dưới dạng đó:

Bài 66 (trang 34 SGK Toán 7 Tập 1): Giải thích vì sao các phân số sau viết được dưới dạng số thập phân vô hạn tuần hoàn rồi viết chúng dưới dạng đó

Bài 67 (trang 34 SGK Toán 7 Tập 1):

Hãy tìm số nguyên tố x có một chữ số để A viết được dưới dạng số thập phân hữu hạn. Có thể điền đươc mấy số như vậy?
Bài 68 (trang 34 SGK Toán 7 Tập 1): a) Trong các phân số sau đây phân số nào viết được dưới dạng số thập phân hữu hạn phân số nào viết được dưới dạng sô thập phân vô hạn tuần hoàn. Giải thích.
![]()
b) Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn (viết gọn với chu kì trong dấu ngoặc)
Đúng 0
Bình luận (0)
Viết các phân số \(\frac{1}{4}; - \frac{2}{{11}}\) dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)
Đúng 0
Bình luận (0)






























