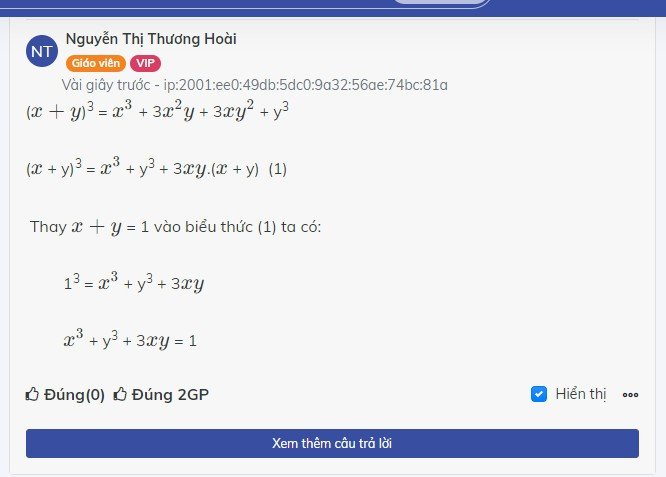
với x+y=1,giá trị của biểu thức :x^3+y^3+3xy là

Những câu hỏi liên quan
a)Cho x+y=1.Tính giá trị của biểu thức x3+y3+3xy
b)Cho x-y=1.Tính giá trị của biểu thức x3-y3-3xy
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức sau: K=x^3+y^3+3xy với x+y=1
Ta có
\(\left(x+x\right)^3=x^3+3x^2y+3xy^2+y^3=x^3+y^3+3xy\left(x+y\right)\)
\(\Rightarrow x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(\Rightarrow K=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\) Với x+y=1
\(\Rightarrow K=1^3-3xy+3xy=1\)
Đúng 1
Bình luận (0)
a) cho x + y = 1 . tính giá trị biểu thức x3 + y3 + 3xy
b) cho x-y= 1. tính giá trị của biểu thức x3 - y3 - 3xy
a) \(x+y=1\)
=> \(\left(x+y\right)^3=1\)
<=> \(x^3+y^3+3xy\left(x+y\right)=1\)
<=> \(x^3+y^3+3xy=1\)
b) \(x-y=1\)
=> \(\left(x-y\right)^3=1\)
<=> \(x^3-y^3-3xy\left(x-y\right)=1\)
<=> \(x^3-y^3-3xy=1\)
Đúng 0
Bình luận (0)
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1
Đúng 0
Bình luận (0)
1)Với x+y=1, giá trị của biểu thức x^3+y^3 +3xy bằng bao nhiêu
2)cho hình thang ABCD có góc A= góc D =90 độ, M là trung điểm của BC khi đó góc MAB…….. góc MDC
3)với x - y = 1 thì giá trị của biểu thức x^3 - y^3 - 3xy
4)nếu a + b + c = 0 và abc = -2 thì a^3 + b^3 + c^3 bằng bao nhiêu
Với x+y=1, giá trị của biểu thức x^3+y^3 +3xy bằng bao nhiêu
x+y=1 => (x+y)^3=1 <=> x^3+3x^2y+3xy^2+y^3=1
<=> x^3+y^3+3xy(x+y)=1
<=> x^3+y^3+3xy=1 Do x+y=1
Đúng 0
Bình luận (0)
Cho x+y=1 .tính giá trị biểu thức x3 + y3 +3xy và x-y=1 .Tính giá trị biểu thức x3 - y3-3xy
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
Đúng 0
Bình luận (0)
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
mọi người ơi cần gấp nhé
1)Với x+y=1, giá trị của biểu thức x^3+y^3 +3xy bằng bao nhiêu
2)cho hình thang ABCD có góc A= góc D =90 độ, M là trung điểm của BC khi đó góc MAB…….. góc MDC
3)với x - y = 1 thì giá trị của biểu thức x^3 - y^3 - 3xy
4)nếu a + b + c = 0 và abc = -2 thì a^3 + b^3 + c^3
2, kéo dài tia Am về phía M cắt DC tại F
Do ABCD là hình thang có góc A=góc D=90 độ nên AB song song CD
=> AB cũng song song DF => góc MCF = góc MBA ( so le trong )
xét tam giác MAB và tam giác MFC có:
góc CMF= góc AMB ( đối đỉnh)
MB=MC( M là trung điểm BC)
góc ABM= góc MCF( chứng minh trên)
=> tam giác MAB= tam giác MFC ( g.c.g)
=> MA=MF
Xét ta giác ADF có DM là đương trung tuyến ứng với cạnh huyền AF => DM=AM=MF
=> tam giác ADM và tam giác MDF cân tại M => góc MAD= góc MDA= 45 độ => góc MAB = 90 độ - góc MAD và góc MDC = 90 độ - góc MDA <=> góc MAB= 45 độ và góc MDC= 45 độ => góc MAB=góc MDC
3, Tương tự như câu 1
4, a+b+c=0 => a+b=-c => (a+b)^3=-c^3 <=> a^3+3a^2b+3ab^2+b^3=-c^3 => a^3+b^3+c^3=-3a^2b-3ab^2
<=> a^3+b^3+c^3= -3ab(a+b) Mà a+b=-c nên thay vào ta có:
a^3+b^3+c^3=-3ab(-c)=3abc mà abc=-2 => a^3+b^3+c^3=-6
Đúng 0
Bình luận (0)
Giá trị của biểu thức
1
/
3
x
2
y
2
-
3
x
y
t
ạ
i
x
1
,
y
-
3
là: A. 12 B. 11 C. 10 D. 9
Đọc tiếp
Giá trị của biểu thức 1 / 3 x 2 y 2 - 3 x y t ạ i x = 1 , y = - 3 là:
A. 12
B. 11
C. 10
D. 9
Thay x = 1, y = -3 vào biểu thức ta có 1/3. 12.(-3)2, - 3.1.(-3) = 12.
Chọn A
Đúng 0
Bình luận (0)