Ta không có \(2^m+2^n=2^{m+n}\) với mọi số nguyên dương m,n . Nhưng có những số nguyên dưowng m,n có tính chất trên . Tìm các số đó

Những câu hỏi liên quan
Ta không có \(2^m+2^n=2^{m+n}\)với mọi số nguyên dương m,n. Nhưng có những số nguyên dương m,n có tính chất trên. Tìm các số đó
Ta có :
\(2^m+2^n=2^{m+n}\Leftrightarrow2^{m+n}-2^m-2^n=0\)
\(\Leftrightarrow2^m.\left(2^n-1\right)-\left(2^n-1\right)=1\Leftrightarrow\left(2^n-1\right).\left(2^m-1\right)=1\)
\(\Leftrightarrow\hept{\begin{cases}2^n-1=1\\2^m-1=1\end{cases}}\Leftrightarrow m=n=1\)
Vậy m = 1 ; n = 1
Đúng 1
Bình luận (0)
<br class="Apple-interchange-newline"><div id="inner-editor"></div>2m+2n=2m+n⇔2m+n−2m−2n=0
⇔2m.(2n−1)−(2n−1)=1⇔(2n−1).(2m−1)=1
⇔{
| 2n−1=1 |
| 2m−1=1 |
Vậy m = 1 ; n = 1
Đúng 4 Sai 0 Shit đã chọn câu trả lời này.
Đúng 1
Bình luận (0)
Ta không có 2m + 2n = 2m+n với mọi số nguyên dương m, n. Nhưng có những số nguyên dương m, n có tính chất trên. Tìm các số đó
\(2^m+2^n=2^{m+n}\)--->Chia 2 vế cho 2n
\(\Rightarrow2^{m-n}+1=2^m\Leftrightarrow2^m-2^{m-n}=1\)
\(\Leftrightarrow2^{m-n}\left(2^n-1\right)=1\)---> Các lũy thừa số mũ tự nhiên của 2 không thể bé hơn 1 nên pt chỉ có nghiệm khi:
\(\hept{\begin{cases}2^{m-n}=1\\2^n-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}2^{m-n}=2^0\\2^n=2^1\end{cases}\Leftrightarrow}\hept{\begin{cases}m-n=0\\n=1\end{cases}\Rightarrow}m=n=1}\)
\(2^m+2^n=2^{m+n}\Leftrightarrow2^m.2^n-2^m-2^n+1=1\)
\(2^m\left(2^n-1\right)-\left(2^n-1\right)=1\Leftrightarrow\left(2^m-1\right)\left(2^n-1\right)=1\)
Vì \(2^m-1\)và \(2^n-1\)đều lớn hơn 0 nên ta chỉ có một trường hợp \(\hept{\begin{cases}2^m-1=1\\2^n-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\n=1\end{cases}}}\)
ta không có \(2^m+2^n=2^{m+n}\) với mọi số nguyên dương m,n .Nhưng có những số nguyên m,n có tính chất trên. Tìm các số nguyên m,n thỏa mãn
a)
x2 - 4x + 3 = x2 - x - 3x + 3
= x(x - 1) - 3(x - 1) = (x -1)(x - 3)
b)
x2 + 5x + 4 = x2 + 4x + x + 4
= x(x + 4) + (x + 4)
= (x + 4)(x + 1)
Đúng 0
Bình luận (0)
ta không có 2m+2n =2m+n với mọi số nguyên dương m,n. nhưng cũng có 1 số trường hợp số nguyên dương m,n có tính chất trên. hãy tìm các số đó
Nếu 2m + 2n = 2m+n
thì: 2m + 2n = 2m.2n
=> 2m = 2m.2n - 2n
=> 2m = 2n.(2m-1)
=> 1 = (2n - 1).(2m-1)
còn lại bạn lập bảng tự làm nhé
Đúng 0
Bình luận (0)
1) Ta không có 2^m +2^n 2^m+n với mọi số nguyên dương m,n.Nhưng có những số nguyên dương m,n thoả mãn đẳng thức đó 2)Viết phân số 1/4 thành tổng của hai phân số có tử bằng 1 và mẫu dương khác nhau 3)Thay 1/4 thành 1/6 4)Tìm hai số tự nhiên sao cho tổng của hai số ấy đúng bằng tích của chúng5)Tìm hai số tự nhiên sao cho tích của hai số ấy gấp 4 lần tổng của chúng
Đọc tiếp
1) Ta không có 2^m +2^n = 2^m+n với mọi số nguyên dương m,n.Nhưng có những số nguyên dương m,n thoả mãn đẳng thức đó
2)Viết phân số 1/4 thành tổng của hai phân số có tử bằng 1 và mẫu dương khác nhau
3)Thay 1/4 thành 1/6
4)Tìm hai số tự nhiên sao cho tổng của hai số ấy đúng bằng tích của chúng
5)Tìm hai số tự nhiên sao cho tích của hai số ấy gấp 4 lần tổng của chúng
1) cô hướng dẫn rồi
2)ta có 1/4 =3/12=1/12+1/6
3)ta có 1/6=3/18=1/9+1/18
4) giống câu 1)
Đúng 0
Bình luận (0)
cho 2n+1 số nguyên , trong đó có đúng mốt số 0 và các số 1,2,3,...,n mỗi số xuất hiện 2 lần. chứng minh rằng với mọi số tự nhiên n ta luôn sắp xếp được 2n+1 số nguyên trên thành sao cho với mọi m=1,2,...,n có đúng m số nằm giữa hai số m
Cho số nguyên dương N (N ≤ 104). Gọi M là tổng của N với các chữ số của nó. Khi đó ta gọi N là nguồn của M.Ví dụ : N 245, khi đó 245 + 2 + 4 + 5 256. Như vậy 245 là nguồn của 256. Có những số không có nguồn và có những số có nhiều nguồn. Ví dụ, số 216 có 2 nguồn là 198 và 207.Cho số nguyên M (M ≤ 104). Hãy tìm nguồn nhỏ nhất của nó. Nếu M không có nguồn thì ghi ra 0.Input : gồm một số M duy nhấtOutput : gồm một số duy nhất là nguồn của M hoặc số 0 nếu M không có nguồn.InputOutput216198Làm pasc...
Đọc tiếp
Cho số nguyên dương N (N ≤ 104). Gọi M là tổng của N với các chữ số của nó. Khi đó ta gọi N là nguồn của M.
Ví dụ : N = 245, khi đó 245 + 2 + 4 + 5 = 256. Như vậy 245 là nguồn của 256. Có những số không có nguồn và có những số có nhiều nguồn. Ví dụ, số 216 có 2 nguồn là 198 và 207.
Cho số nguyên M (M ≤ 104). Hãy tìm nguồn nhỏ nhất của nó. Nếu M không có nguồn thì ghi ra 0.
Input : gồm một số M duy nhất
Output : gồm một số duy nhất là nguồn của M hoặc số 0 nếu M không có nguồn.
| Input | Output |
| 216 | 198 |
Làm pascal nha mn giúp mình với
Cho số nguyên dương N (N ≤ 104). Gọi M là tổng của N với các chữ số của nó. Khi đó ta gọi N là nguồn của M.Ví dụ : N 245, khi đó 245 + 2 + 4 + 5 256. Như vậy 245 là nguồn của 256. Có những số không có nguồn và có những số có nhiều nguồn. Ví dụ, số 216 có 2 nguồn là 198 và 207.4). Hãy tìm nguồn nhỏ nhất của nó. Nếu M không có nguồn thì ghi ra 0.Input : gồm một số M duy nhấtOutput : gồm một số duy nhất là nguồn của M hoặc số 0 nếu M không có nguồn.InputOutput216198Làm pascal nha mn giúp mình với
Đọc tiếp
Cho số nguyên dương N (N ≤ 104). Gọi M là tổng của N với các chữ số của nó. Khi đó ta gọi N là nguồn của M.
Ví dụ : N = 245, khi đó 245 + 2 + 4 + 5 = 256. Như vậy 245 là nguồn của 256. Có những số không có nguồn và có những số có nhiều nguồn. Ví dụ, số 216 có 2 nguồn là 198 và 207.
4). Hãy tìm nguồn nhỏ nhất của nó. Nếu M không có nguồn thì ghi ra 0.
Input : gồm một số M duy nhất
Output : gồm một số duy nhất là nguồn của M hoặc số 0 nếu M không có nguồn.
| Input | Output |
| 216 | 198 |
Làm pascal nha mn giúp mình với
program tim_nguon_nho_nhat;
const
MAX_NUMBER = 10000;
var
M, nguon_nho_nhat: Integer;
function TinhTongChuSo(num: Integer): Integer;
var
sumOfDigits: Integer;
begin
sumOfDigits := 0;
while num > 0 do
begin
sumOfDigits := sumOfDigits + (num mod 10);
num := num div 10;
end;
TinhTongChuSo := sumOfDigits;
end;
function TimNguonNhoNhat(M: Integer): Integer;
var
N, M_temp, M_digits, nguon_nho_nhat: Integer;
begin
M_temp := M;
nguon_nho_nhat := MAX_NUMBER;
for N := 1 to M_temp do
begin
M_digits := TinhTongChuSo(N) + N;
if M_digits = M_temp then
begin
if N < nguon_nho_nhat then
nguon_nho_nhat := N;
end;
end;
if nguon_nho_nhat = MAX_NUMBER then
TimNguonNhoNhat := 0
else
TimNguonNhoNhat := nguon_nho_nhat;
end;
begin
Readln(M);
nguon_nho_nhat := TimNguonNhoNhat(M);
if nguon_nho_nhat = 0 then
Writeln('0')
else
Writeln('Nguon nho nhat cua ', M, ' la ', nguon_nho_nhat);
end.
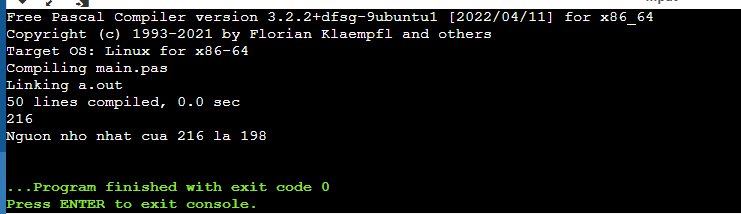
Đúng 1
Bình luận (0)
tìm mọi cặp số nguyên dương (M;N) thỏa mãn tất cả các điều kiện:
1) M và N là những số nguyên dương có bốn chữ số;
2) M và N là những số chính phương;
3) Chỉ có hai cặp số tương ứng ở cùng một vị trí của M và N bằng nhau;
4) Với các chữ số còn lại, chữ số của M lớn hơn chữ số tương ứng cùng vị trí của N là 1 đơn vị
Ví dụ (M;N)=(2601;2500)


















