Tìm 3 số a,b,c biết chúng tỉ lệ nghịch với \(\frac{8}{7}\),\(\frac{8}{9}\),\(\frac{5}{7}\) và hiệu của b và a là 20 ?

Những câu hỏi liên quan
Tìm 3 số a, b, c lần lượt tỉ lệ nghịch với \(\frac{8}{7};\frac{8}{9};\frac{5}{7}\) và hiệu của a và b là 20
Theo đề ra ta có:
\(\frac{8a}{7}=\frac{8b}{9}=\frac{5c}{7}hay\frac{a}{\frac{7}{8}}=\frac{b}{\frac{9}{8}}=\frac{c}{\frac{7}{5}}\)
và \(a-b=20\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{7}{8}}=\frac{b}{\frac{9}{8}}=\frac{c}{\frac{7}{5}}=\frac{a-b}{\frac{7}{8}-\frac{9}{8}}=\frac{20}{\frac{-1}{4}}=-80\)
\(\rightarrow a=-80\cdot\frac{7}{8}=-70\)
\(\rightarrow b=-80\cdot\frac{9}{8}=-90\)
\(\rightarrow c=-80\cdot\frac{7}{5}=-112\)
Đúng 0
Bình luận (0)
Tìm 3 số a,b,c biết chúng lần lượt tỉ lệ nghịch với 8/7 ,8/9,5/7 và hiệu của b và a la 20
Tìm a và b biết tổng hiệu tích của chúng tỉ lệ nghịch với \(\frac{1}{7},5,\frac{5}{144}\)
Tìm ba số a,b,c biết chúng tỉ lệ nghịch với \(\frac{1}{2};\frac{1}{5};\frac{1}{7}\)và a+b-2c=70
Theo bài ra, ta có:
\(\frac{1}{2}a=\frac{1}{5}b=\frac{1}{7}c\Rightarrow\frac{a}{2}=\frac{b}{5}=\frac{c}{7}\)
Áp dụng tích chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{2}=\frac{b}{5}=\frac{c}{7}=\frac{2c}{14}=\frac{a+b-2c}{2+5-14}=\frac{70}{-7}=-10\)
\(\Rightarrow\hept{\begin{cases}a=-10.2=-20\\b=-10.5=-50\\c=-10.7=-70\end{cases}}\)
Đúng 0
Bình luận (0)
Biết 3 số a,b,c chúng tỉ lệ nghịch với \(\frac{1}{2};\frac{1}{5};\frac{1}{7}\) và a+b-2c=70. Giá trị a+b-c=................
các bạn làm và giải đầy đủ hộ mk nha!!!
vì a,b,c tỉ lệ nghịch với 1/2;1/5;1/7 nên a/2=b/5=c/7. Hay a/2=b/5=2c/14
ADTCCDTSBN TA CÓ
a/2=b/5=2c/14=a+b-2c/2+5-14=70/-7=-10
Suy ra a/2=-10 nên a=-20
b/5=-10 nên b=-50
2c/14=-10 nên c=-70
Đúng 0
Bình luận (0)
Biết 3 số a,b,c chúng tỉ lệ nghịch với 1/2 ; 1/5 ; 1/7
=> a/2 = b/5 = c/7
=> a/2 = b/5 = -2c/-14
Áp dụng tc dãy tỉ số = nhau ta đc :
a/2 = b/5 = -2c/-14 = (a+b-2c)/(2+5-14) = 70/-7 = -10
=>a= -20 ; b= -50 ; c = -70
=> a+b-c = 0
Đúng 0
Bình luận (0)
Tìm 3 phân số tối giản biết tổng của chúng bằng \(5\frac{25}{63}\). Tử của chúng tỉ lệ nghịch với 20; 4; 5 và mẫu của chúng tỉ lệ thuận với 1; 3; 7
bạn bấm vào đúng 0 sẽ ra kết quả
mình làm bài này rồi
Đúng 0
Bình luận (0)
bạn bấm vào đúng 0 sẽ ra kết quả
mình làm bài này rồi
Đúng 0
Bình luận (0)
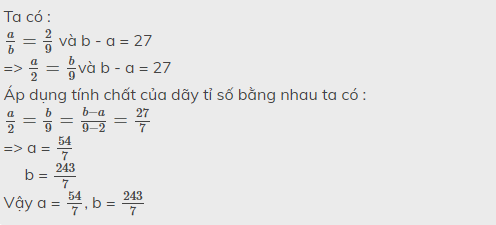
1. Cho a và b là 2 số tỉ lệ nghịch với 4,5 và b - a = 27. Tính a và b
2. Cho xyz tỉ lệ nghịch với 1/3, 1/2, 1/5 và x + 2y - z = 8. Tìm xyz
3. Tìm a, b, c biết a và b tỉ lệ nghịch với 1/3 và 1/2; a và c tỉ lệ nghịch với 1/5 và 1/7 và a + b + c = 184
giúp mình ạ
\(1,4a=5b\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{b-a}{4-5}=\dfrac{27}{-1}=-27\\ \Leftrightarrow\left\{{}\begin{matrix}a=-135\\b=-108\end{matrix}\right.\\ 2,\dfrac{1}{3}x=\dfrac{1}{2}y=\dfrac{1}{5}z\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x+2y-z}{3+4-5}=\dfrac{8}{2}=4\\ \Leftrightarrow\left\{{}\begin{matrix}x=12\\y=8\\z=20\end{matrix}\right.\\ 3,\dfrac{1}{3}a=\dfrac{1}{2}b;\dfrac{1}{5}a=\dfrac{1}{7}c\\ \Leftrightarrow\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{a+b+c}{15+10+21}=\dfrac{184}{46}=4\\ \Leftrightarrow\left\{{}\begin{matrix}a=60\\b=40\\c=84\end{matrix}\right.\)
Đúng 2
Bình luận (1)
1, So sánh : Cfrac{1}{1!}+frac{1}{2!}+frac{1}{3!}+...+frac{1}{2019!}vtext{ới}frac{7}{4}(Ktext{í}hitext{ệu}n!1.2.3...n) 2, Chofrac{a^2+b^2}{c^2+d^2}frac{ab}{cd}vtext{ới}a,b,c,dne0.CMR:frac{a}{b}frac{c}{d}hotext{ặc}frac{a}{b}frac{d}{c}3, Tìm2 số dương biết tổng hiệu tích của chúng lần lượt tỉ lệ nghịch với 15;60 và 84, Cho đa thứ f(x)ax2-bx+c với a,b,c là các số nguyên và a khác 0 sao cho f(9) chia hết cho 5 và f(5) chia hết cho 9. CMR:f(104) chia hết cho 45.5, Tìm các số nguyên tố a,b,c t...
Đọc tiếp
1, So sánh : \(C=\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{2019!}v\text{ới}\frac{7}{4}(K\text{í}hi\text{ệu}n!=1.2.3...n)\)
2, Cho\(\frac{a^2+b^2}{c^2+d^2}=\frac{ab}{cd}v\text{ới}a,b,c,d\ne0.CMR:\frac{a}{b}=\frac{c}{d}ho\text{ặc}\frac{a}{b}=\frac{d}{c}\)
3, Tìm2 số dương biết tổng hiệu tích của chúng lần lượt tỉ lệ nghịch với 15;60 và 8
4, Cho đa thứ f(x)=ax2-bx+c với a,b,c là các số nguyên và a khác 0 sao cho f(9) chia hết cho 5 và f(5) chia hết cho 9. CMR:f(104) chia hết cho 45.
5, Tìm các số nguyên tố a,b,c thõa mãn a2+5ab+b2=7c
GIẢ SỬ \(\frac{A}{B}=\frac{C}{D}\)
ĐẶT\(\frac{A}{B}=\frac{C}{D}=T\)=>A = BT , C = DT
TA CÓ\(\frac{\left(A^2+B^2\right)}{\left(C^2+D^2\right)}=\frac{\left(\left(B\cdot T\right)^2+B^2\right)}{\left(\left(D\cdot T\right)^2+D^2\right)}=\frac{\left(B^2\cdot\left(T^2+1\right)\right)}{\left(D^2\cdot\left(T^2+1\right)\right)}=\frac{B^2}{D^2}=\left(\frac{B}{D}\right)^2\left(1\right)\)
LẠI CÓ\(\frac{\left(A\cdot B\right)}{\left(C\cdot D\right)}=\frac{\left(B\cdot T\cdot B\right)}{\left(D\cdot T\cdot D\right)}=\frac{B^2}{D^2}=\left(\frac{B}{D}\right)^2\left(2\right)\)
TỪ (1) VÀ (2) \(\Rightarrow\frac{\left(A^2+B^2\right)}{\left(C^2+D^2\right)}=\frac{\left(A\cdot B\right)}{\left(C\cdot D\right)}\)( THÕA ĐỀ )
=> ĐIỀU GIẢ SỬ ĐÚNG => DPCM
sao ban ko k cho minh
1/ Tìm 2 phân số tối giản biết hiệu của chúng là \(\frac{3}{106}\) và các tử tỉ lệ với 3; 5. Các mẫu tỉ lệ với các số 4; 7.
2/ Cho tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\) . Hãy chứng tỏ:
a) \(\frac{a}{b}=\frac{c}{d}=\frac{-2a+7c}{-3b+7d}\)
b) \(\frac{a^2}{b^2}=\frac{3a^2-2ac}{2b^2-2bd}\)