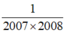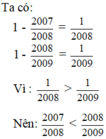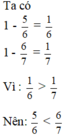CMR : tổng : P= 20062007 +20072008+20082009 chia hết cho 5

Những câu hỏi liên quan
Kết quả của phép tính
2007
2008
-
2006
2007
là: A.
1
2007
×
2008
B.
1
2007
C.
1
2008
D.
2
2007
×
2008
Đọc tiếp
Kết quả của phép tính 2007 2008 - 2006 2007 là:
A. 1 2007 × 2008
B. 1 2007
C. 1 2008
D. 2 2007 × 2008
Kết quả của phép tính 2007 2008 - 2006 2007 là:
Kết quả của phép tính
2007
2008
-
2006
2007
là: A.
1
2007
×
2008
B.
1
2007
C.
1
2008
D.
2
2007
×
2008
Đọc tiếp
Kết quả của phép tính 2007 2008 - 2006 2007 là:
A. 1 2007 × 2008
B. 1 2007
C. 1 2008
D. 2 2007 × 2008
So sánh các phân số sau: (Không quy đồng tử số hoặc mẫu số)
2007 2008 và 2008 2009 ; 5 6 và 6 7
Bài 1: So sánh A và B biết
a A = -1/2011 -3/112 - 5/ 113 - 7/114 và B= 1/2011 - 7/112 -5/113 -3/ 114
b A= 2006/2007 -2007/2008 + 2008/2009 -2009/2010 và B= -1/ 20062007-1/ 20082009
1, CMR: tổng của 3 số tự nhiên liên tiếp chia hết cho 3, tổng của 5 số tự nhiên liên tiếp thì chia hết cho 5
2,CMR:
+ tổng của 3 số chẵn liên tiếp thì chia hết cho 6
+ tổng của 3 số lẻ liên tiếp thì không chia hết cho 6
+ tổng của 5 số chẵn liên tiếp thì chia hết cho 10 còn tổng của 5 số lẻ liên tiếp thì chia 10 dư 5
1.Gọi 3 số tự nhiên liên tiếp là a, a+1, a+2
Có: a+(a+1)+(a+2)=a+a+a+1+2=3a+3=3(a+1)\(⋮\) 3
Vậy ...
Gọi 5 số tự nhiên liên tiếp là a, a+1, a+2,a+3,a+4
Có : a+(a+1)+(a+2)+(a+3)+(a+4)= a+a+a+a+a+1+2+3+4=5a+10=5(a+2)\(⋮\) 5
Vậy ...
2.
+)Gọi 3 số chẵn liên tiếp là a, a+2,a+4
Có : a+(a+2)+(a+4)=a+a+a+2+4=3a+6
mà a là số chẵn nên 3a \(⋮\) 6
\(\Rightarrow\) 3a+6\(⋮\) 6
Vậy ....
+) ngược lại ý đầu
+)Gọi 5 số chẵn liên tiếp là a, a+2,a+4 , a-2,a-4
Có : a+(a+2)+(a+4)+(a-2)+(a-4)=a+a+a+a+a+2+4-2-4=5a
mà a là số chẵn nên 5a \(⋮\) 10
\(\Rightarrow\) 5a\(⋮\) 10
Vậy ....
+) ngược lại ý 3
CMR tổng của 3 số liên tiếp chia hết cho 3
CMR tổng của 5 số liên tiếp chia hết cho5
Gọi 3 STN liên tiếp là a;a+1;a+2(a là STN)
Ta có tổng 3 STN liên tiếp là:a+(a+1)+(a+2)=3a+3=3(a+1) chia hết cho 3(đpcm)
Gọi 5 STN liên tiếp là:x;x+1;x+2;x+3;x+4(x là STN)
Ta có tổng 5 STN liên tiếp là:x+(x+1)+(x+2)+(x+3)+(x+4)=5x+10=5(x+2) chia hết cho 5(đpcm)
Đúng 0
Bình luận (0)
CMR: Tổng ba số tự nhiên liên tiếp chia hết cho 3, tổng của 5 số liên tiếp chia hết cho 5
Gọi 3 số tự nhiên liên tiếp là: n; n+1; n+2
Tổng 3 số là: n+ ( n+1) + (n+2)
= n + n +1 + n+2
= n.3 + 3
Vì n.3+3 chia hết cho 3 nên n+ ( n+1) + (n+2)\(⋮\)3
Vậy...
Ta có : a+1 ; a+2 ; a+3 là 3 số tn liên tiếp (a thuộc n)
=>a+1+a+2+a+3=3a+6 =3.(a+2)
do 3.(a+2) chia hết cho 3
=> đpcm
Lại có : a+1;a+2;a+3;a+4;a+5 là 5 số tn liên tiếp (a thuộc n)
=>a+1+a+2+a+3+a+4+a+5=5a+15=5.(a+3)
do5.(a+3) chia hết cho 5
=>đpcm
Lâu lắm r cg ko làm dạng này :))
# Chia hết cho 3
Gọi ba số tự nhiên liên tiếp là a, a+1 và a+2
Ta có tổng 3 số tự nhiên liên tiếp là :
a+(a+1)+(a+2)= a+a+1+a+2 = 3a +3 = 3(a+1)
Vì 3\(⋮\)3 => 3(a+1) \(⋮\)3
Vậy 3 số tự nhiên liên tiếp chia hết cho 3 (dpcm)
# Cha hết cho 5 : CM tương tự
Xem thêm câu trả lời
CMR tổng của 3 số tự nhiên liên tiếp chia hết cho 3, tổng của 5 số tự nhiên liên tiếp chia hết cho 5
-Gọi 3 số tự nhiên liên tiếp la a;a+1;a+2
Tổng 3 số trên là:
a+(a+1)+(a+2)=(a+a+a)+(1+2)=a.3+3 chia hết cho 3
Đúng 0
Bình luận (0)
Cho 4 STN ko chia hết cho 5, khi chia cho 5 đc những số dư khác nhau. CMR tổng của chúng chia hết cho 5