Cho hình vẽ sau , biết ABC+BCD+CDE360. Chứng tỏ AB//DE. A B C D E
Đọc tiếp
Cho hình vẽ sau , biết ABC+BCD+CDE=360. Chứng tỏ AB//DE.
Những câu hỏi liên quan
Cho hình vẽ bên, biết: góc ABC=120 độ, góc BCD=30 độ, góc CDE= 150độ. Chứng tỏ rằng AB//DE? (Giải thích cụ thể cách làm)
Hình nào?
không có hình thì làm làm sao được?
Bạn vẽ hình đi :)
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết:
BAC+CDE-ACD=180°
Chứng tỏ AB//DE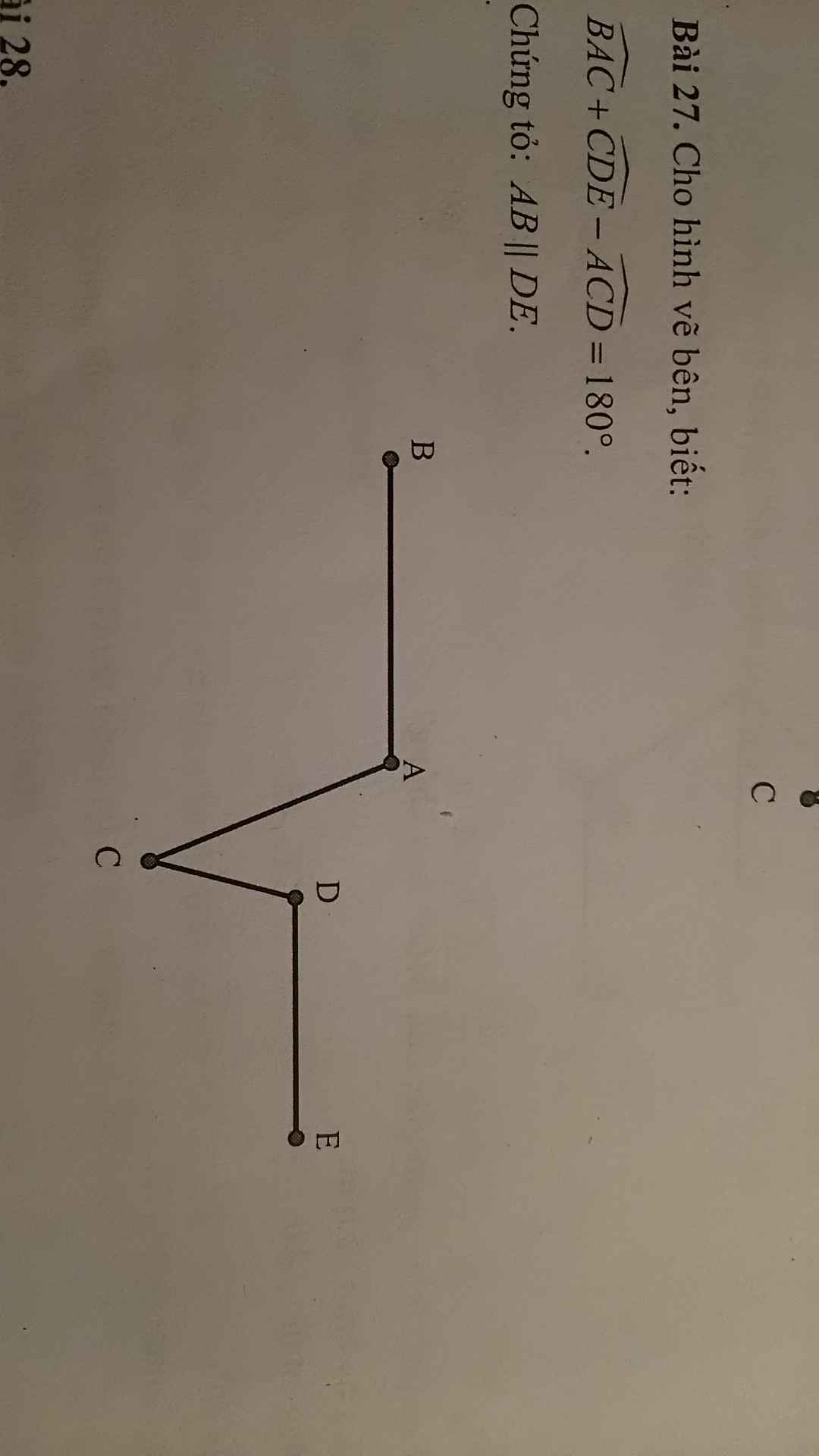
Cho ABC có AB= 3cm, AC= 4cm, BC- 5cm
a) Vẽ hình, ghi GT,KL
b) Chứng tỏ tam giác ABC vuông tại A
c) Vẽ phân giác BD( D thuộc AC), Gọi E là hình chiếu của D trên BC (E thuộc BC). Chứng minh DA=DE
d) ED cắt AB tại F. Chứng minh tam giác ABC = tam giác EDC rồi suy ra DF> DE
Cho hình vẽ, biết AB//DE
a) chứng minh rằng ACD=BAC+CDE
b)tính góc ACD biết góc ABC=60độ, góc CDE=32 độ
?? C lấy đâu ra vậy bạn ?
Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm. a) Chứng tỏ tam giác ABC vuông tại A. b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE BC (E BC). Chứng minh DA = DE. c) ED cắt AB tại F. Chứng minh ADF = EDC rồi suy ra DF > DE.
Cho tam giác ABC, tia phân giác của góc A cắt BC tại D. Trên tia AC lấy điểm E sao cho AE = AB.
a) Chứng minh rằng DE = DB
b) gọi giao của BA và ED là M, c/m BDM=CDE
c) c/m AD vuông MC
nhớ vẽ hình nha
a) Xét \(\Delta ABD\) và \(\Delta AED\) có :
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
=> \(\Delta ABD\) =\(\Delta AED\) (c-g-c)
=> DE=DB ; \(\widehat{ABD}=\widehat{AED}\)
b)Có : \(\widehat{ABD}+\widehat{MBD}=180^o\)
\(\widehat{AED}+\widehat{DEC}=180^o\)
mà \(\widehat{ABD}=\widehat{AED}\) => \(\widehat{MBD}=\widehat{DEC}\)
Xét \(\Delta MDBvà\Delta CDE\) có :
\(\widehat{MBD}=\widehat{DEC}\)
DE=DB
\(\widehat{MBD}=\widehat{CDE}\)
=> \(\Delta MDB=\Delta CDE\left(g-c-g\right)\)
c) Có : AB=AE ( \(\Delta ABD\) =\(\Delta AED\) )
MB=CE(\(\Delta MDB=\Delta CDE\))
=> AB+BM=AE+EC
=> AM=AC
=> \(\Delta MAC\) cân tại A
mà AD là tia phân giác của góc A
=> AD là đường cao của \(\Delta MAC\)
=> \(AD\perp MC\)
Đúng 3
Bình luận (0)
Cho hình sau. Biết BF vuông góc EF, góc ABC
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
Vẽ lại hình:
Qua C, kẻ đường thẳng MN//AB
MN//AB
=>\(\hat{ABC}+\hat{BCM}=180^0\) (hai góc trong cùng phía)
=>\(\hat{ABC}=180^0-\hat{BCM}\)
Ta có; \(\hat{ABC}+\hat{CDE}=\hat{BCD}+180^0\)
=>\(180^0-\hat{BCM}+\hat{CDE}=\hat{BCD}+180^0\)
=>\(\hat{CDE}-\hat{BCM}=\hat{BCD}\)
=>\(\hat{CDE}=\hat{BCM}+\hat{BCD}=\hat{DCM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên FE//MN
=>FE//AB
Ta có: FE//AB
FE⊥ FB
Do đó: BA⊥BF
Đúng 0
Bình luận (0)
Bài 2 : Cho hình vẽ : a) Biết góc BED + góc BCD + góc CDE + góc DEB = 360 độ . Tính DEB b) Xét xem góc BED và EDC ; xED và EDy có bù nhau không ?
Cho tam giác ABC có AB = 3cm; AC = 5cm; BC = 4cm
a)Chứng tỏ tam giác ABC vuông tại B
b)Vẽ phân giác AD (D thuộc BC).Từ D ,vẽ DE vuông AC (E thuộc AC).Chứng minh: DB=DE
c)ED cắt AB tại F.Chứng minh tam giác BDF = tam giácEDC rồi suy ra DF>DE
d)Chứng minh AB+|BC>DE+AC