Bài 1
cho hình thăng vuông ABCD có góc A=góc D=90độ .gọi E,F lần lượt là trung điểm của Ad,BC.chứng minh
a,tam giác ÀD cân tại F
b, góc BAf= góc CDF
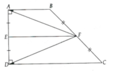
Hình thang ABCD vuông tại A và D. Gọi E, F lần lượt là trung điểm AD, BC. Chứng minh rằng: a) Tam giác AFD cân tại F b) Góc BAF = Góc CDF
vẽ hình nữa ạ
Giải
Vì E là trung điểm AC
F là trung điểm BD
=> EF // CD // AB
=>góc AEF \(\perp\) CEF vuông
Xét \(\Delta\) AEF và CEF có
:/\ AEF = /\ CEF = 90 độ
EF chung
AE = AC (gt)
=> \(\Delta\) AEF = CEF ( cạnh góc cạnh )
=>\(\Delta\) AFD là tam giác cân
b, Vì \(\Delta\)AFD là \(\Delta\)cân nên
\(\Rightarrow\)Góc FAD = góc FDA
Ta có : góc A = góc BAF + góc FAD
Góc D = góc CDF + góc FDA
mà góc A = góc D = 90 độ
=> góc BAF = góc CDF
a)
Xét hình thang ABCD ta có:
- E là trung điểm của AD
- F là trung điểm của BC
=> EF là đường trung bình của hình thang ABCD
\(\Rightarrow EF//AB//CD\)
Mà \(AB\perp AD\Rightarrow EF\perp AD\)
Xét tam giác FAD ta có:
- FE là đường cao ứng với cạnh AD
- FE là đường trung tuyến ứng với cạnh AD
=> Tam giác FAD cân tại F
b)
\(\widehat{BAF}+\widehat{DAF}=90^o\)
\(\widehat{CDF}+\widehat{FDA}=90^o\)
Mà \(\widehat{FAD}=\widehat{FDA}\Rightarrow\widehat{BAF}=\widehat{CDF}\)
Cho hình thang vuông ABCD(góc A=góc D=90độ) gọi F là trung điểm của BC.Chứng minh rằng Góc BAF=góc CDF
Cho hình thang vuông ABCD tại A và D. Gọi E và F lần lượt là trung điểm của AD và BC, chứng minh:
a) Tam giác AFD can tại F
b) góc BAF=góc CDF
cho hình thang vuông ABCD góc A = góc D =90độ gọi F là trung điểm BC
chứng minh rằng góc BAF = góc CDF
Cho hình thang vuông ABCD tại A và D. Gọi E,F lần lượt là trung điểm của AD,BC.
Chứng minh:
a) ADFcân tại F b) \(\widehat{BAF}=\widehat{CDF}\)
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)
Bai 1 : Cho hình bình hành ABCD ; góc BAD = 120 độ ; AB = 2 AD
a) CMR: Tia phân giác của góc ADC đi qua trung điểm E của AB .
b) Gọi F là trung điểm DC . CMR tam giác ADF đều và AD vuông góc với AC
Bài 2: Cho hình bình hành ABCD có BC = 2AB . Gọi M là trung điểm AD. Kẻ CE vuông góc với AB ; E nằm giữa A và B . CMR: góc EMD = 3 góc AEM
Bìa 3: Cho tam giác ABC vuông tại A . Đường cao AH . Từ H kẻ HE , HF vuông góc với AB và AC . Kẻ AI vuông góc với EF ( I \(\in\)BC). CMR: a) I là trung điểm BC
b) Cho tam giác ABC vuông tại A. Đường cao AH. Gọi E, F lần lượt là các hình chiếu của H xuống AB, AC. Gọi I là trung điểm của BC. CMR: AI vuông góc với EF.
Bài 4: Cho tam giác ABC cân tại A . D bất kì thuộc BC . Qua D kẻ đường thẳng vuông góc với BC cắt AB và AC lần lượt tại E,F . Gọi I,K lần lượt là trung điểm của BE và CF .
a) CMR: AKDI là hình bình hành
b) Nêu thêm điều kiện của tam giác ABC và của điểm D để DIAK là hình vuông
Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) DAFD cân tại F;
b) B A F ^ = C D F ^ .
a) Ta có È là đường trung bình của hình thang ABCD.
Þ EF//AB.
Suy ra EF ^ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD Þ ĐPCM.
b) Tam giác AFD cân tại F nên E A F ^ = E D F ^
Suy ra F A B ^ = C D F ^
Bài 2: Cho hình bình hành ABCD có BC = 2AB . Gọi M là trung điểm AD. Kẻ CE vuông góc với AB ; E nằm giữa A và B . CMR: góc EMD = 3 góc AEM
Bìa 3: Cho tam giác ABC vuông tại A . Đường cao AH . Từ H kẻ HE , HF vuông góc với AB và AC . Kẻ AI vuông góc với EF ( I thuộc BC). CMR: a) I là trung điểm BC
b) Cho tam giác ABC vuông tại A. Đường cao AH. Gọi E, F lần lượt là các hình chiếu của H xuống AB, AC. Gọi I là trung điểm của BC. CMR: AI vuông góc với EF.
Bài 4: Cho tam giác ABC cân tại A . D bất kì thuộc BC . Qua D kẻ đường thẳng vuông góc với BC cắt AB và AC lần lượt tại E,F . Gọi I,K lần lượt là trung điểm của BE và CF .
a) CMR: AKDI là hình bình hành
b) Nêu thêm điều kiện của tam giác ABC và của điểm D để DIAK là hình vuông
Bài 1 nếu chứng minh cũng chỉ được góc EMD= 2 góc AEM thôi
Cho hình vuông ABCD có cạnh bằng a. Gọi E, F lần lượt là trung điểm các cạnh AB,BC . Gọi M là giao điểm của CE và DF .A. c/m góc ECB = góc CDF và CE vuông góc DF B.c/m CM.CECF =a C. Gọi K là giao điểm của CM và DA . C/m tam giác MAD cân