một người đàn ông bế 2 đứa con. người đàn bà bế 1 đứa con. hỏi cả hai cộng lại có bao nhiêu đứa ?

Những câu hỏi liên quan
Bốn người đàn ông, hai người đàn bà và một đứa trẻ được xếp ngồi vào bảy chiếc ghế đặt quanh một bàn tròn. Hỏi có bao nhiêu cách xếp sao cho:
a) Đứa trẻ ngồi giữa hai người đàn bà?
b) Đứa trẻ ngồi giữa hai người đàn ông?
a) Xếp hai người đàn bà ngồi cạnh nhau.Có 2 cách.
Sau đó xếp đứa trẻ ngồi vào giữa. Có 1 cách.
Xếp 4 người đàn ông vào 4 ghế còn lại. Có 4! cách.
Theo quy tắc nhân, có 2. 4! = 48 cách.
b) Đầu tiên chọn 2 người đàn ông. Có 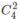 cách.
cách.
Xếp hai người đó ngồi cạnh nhau. Có 2 cách.
Sau đó xếp đứa trẻ vào giữa. Có 1 cách.
Xếp 4 người còn lại vào 4 ghế còn lại. Có 4! cách.
Vậy theo quy tắc nhân, có 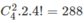 cách.
cách.
Đúng 0
Bình luận (0)
Bốn người đàn ông, hai người đàn bà và một đứa trẻ được xếp ngồi vào 7 chiếc ghế đặt quanh một bàn tròn. Hỏi có bao nhiêu cách xếp sao cho :
a) Đứa trẻ ngồi giữa hai người đàn bà
b) Đứa trẻ ngồi giữa hai người đàn ông
Bốn người đàn ông, hai người đàn bà và một đứa trẻ được xếp vào bảy chiếc ghế đặt quanh bàn tròn. Hỏi có bao nhiêu cách sắp xếp sao cho đứa trẻ ngồi giữa hai người đàn ông.
A. 48
B. 5040
C. 720
D. 288
Bốn người đàn ông, hai người đàn bà và một đứa trẻ được xếp vào bảy chiếc ghế đặt quanh bàn tròn. Hỏi có bao nhiêu cách sắp xếp sao cho đứa trẻ ngồi giữa hai người đàn ông.
A.48.
B.5040.
C.720.
D.288.
Có 17 cái bánh và 17 người dự tiệc.Mỗi người đàn ông ăn 2 cái ,đàn bà ăn 1 cái bánh , mỗi đứa trẻ ăn nửa cái bánh thì vừa hết . Hỏi có bao nhiêu người đàn ông ? Bao nhiêu người đàn bà ? Bao nhiêu đứa trẻ ?
có 17 người đi dự tiệc và 17 cái bánh.mỗi người đàn ông ăn 2 cái bánh ,mỗi người đàn bà ăn 1 cái ,mỗi đứa trẻ ăn nửa cái thì vừa hết.Hỏi có bao nhiêu người đàn ông ?Bao nhiêu người đàn bà ?bao nhiêu đứa trẻ?
Đàn ông Trẻ em Đàn bà
1 2 14
2 4 11
3 6 8
4 8 5
5 10 2
Đúng 0
Bình luận (0)
#)Giải :
Vì có 17 người dự tiệc và 17 cái bánh => trung bình mỗi người ăn 1 cái bánh
=> Trung bình cứ 1 người đàn ông ăn 2 cái bánh, 1 người đàn bà ăn 1 cái bánh thì có 2 đứa trẻ
=> Ta có :
| Đàn ông | Trẻ em | Phụ nữ |
| 1 | 2 | 14 |
| 2 | 4 | 11 |
| 3 | 6 | 8 |
| 4 | 8 | 5 |
| 5 | 10 | 2 |
Đúng 0
Bình luận (0)
Gọi số đàn ông là a , số đàn bà là b , số đứa trẻ là c
Ta có : \(a+b+c=17\) \((1)\)
Mặt khác ta có : \(2\times a+b+c:2=17\)
\(\Rightarrow4\times a+2\times b+c=34\)
\(\Rightarrow3\times a+b+(a+b+c)=34\)
Thay \(a+b+c=17\)ta có : \(3\times a+b+17=34\)
\(\Rightarrow3\times a+b=17\)
* Nếu a = 1 thì \(3\times1+b=17\Leftrightarrow3+b=17\Leftrightarrow b=14\)
Lại có : \(2\times a+b+c:2=17\)
Thay a = 1 , b = 14 ta có : \(2\times1+14+c:2=17\)
\(\Rightarrow c:2=17-14-2\)
\(\Rightarrow c:2=3-2=1\Leftrightarrow c=2\)
Vậy có 1 người đàn ông , 14 người đàn bà , 2 đứa trẻ
Làm tiếp đi nhé :v ra nhiều lắm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Một người đàn ông có 2 đứa con trai. Người thứ nhất nặng 30,5 kg. Hỏi người thứ hai cân nặng bao nhiêu, biết cân nặng của cả ba bố con là 164 kg.
Xếp ngẫu nhiên ba người đàn ông, hai người đàn bà và một đứa bé vào ngồi trên 6 cái ghế, xếp thành hàng ngang. Tính xác suất sao cho
a) Đứa bé ngồi giữa hai người đàn bà;
b) Đứa bé ngồi giữa hai người đàn ông.
Không gian mẫu gồm các hoán vị của 6 người. Vậy n(Ω) = 6!
Kí hiệu A là biến cố : " Đứa bé được xếp giữa hai người đàn bà ";
B là biến cố : " Đứa bé được xếp giữa hai người đàn ông ".
a) Để tạo nên một cách xếp mà đứa bé được xếp giữa hai người đàn bà, ta tiến hành như sau :
- Xếp đứa bé ngồi vào ghế thứ hai đến ghế thứ năm. Có 4 cách.
- Ứng với mỗi cách xếp đứa bé, có 2 cách xếp hai người đàn bà.
- Khi đã xếp hai người đàn bà và đứa bé, xếp ba người đàn ông vào các chỗ còn lại. Có 3! cách.
Theo quy tắc nhân, ta có n(A) = 4.2.3! = 48.
Từ đó: 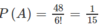
b) Để tạo nên một cách xếp mà đứa bé ngồi giữa hai người đàn ông, ta tiến hành như sau :
- Xếp đứa bé vào các ghế thứ hai đến thứ năm. Có 4 cách.
- Chọn hai trong số ba người đàn ông. Có 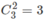 cách.
cách.
- Xếp hai người đàn ông ngồi hai bên đứa bé. Có 2 cách.
- Xếp ba người còn lại vào ba chỗ còn lại. Có 3! cách. Theo quy tắc nhân, ta có
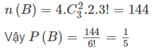
Đúng 0
Bình luận (0)
Số cách xếp 3 người đàn ông, 2 người đàn bà và 1 đứa trẻ ngồi vào ghế xếp quanh một bàn tròn sao cho đứa trẻ ngồi giữa hai người đàn ông là :
A. 6
B. 72
C. 120
D. 36
Đáp án D
Phương pháp: Sử dụng phương pháp buộc : Buộc 2 người đàn ông và 1 đứa trẻ thành 1 buộc, sao cho đứa trẻ ngồi giữa hai người đàn ông.
Cách giải: Buộc 2 người đàn ông và 1 đứa trẻ thành 1 buộc, sao cho đứa trẻ ngồi giữa hai người đàn ông.
Chọn 2 người đàn ông có C 3 2 = 3 cách chọn, 2 người đàn ông có thể đổi chỗ cho nhau nên có 2! = 2 cách xếp.
Khi đó ta coi bài toán thành xếp 4 người vào một bàn tròn.
Cố định 1 người, số cách xếp 3 người còn lại là 3! = 6 cách.
Vậy có 3.2.6 = 36 cách.
Đúng 0
Bình luận (0)













