tìm số tự nhiên có 3 chữ số biết số đó là bội của 18 và các chữ số của nó tỉ lệ với 1.2.3

Những câu hỏi liên quan
Tìm số tự nhiên có 3 chữ số, biết rằng số đó là bội của 18 và các chữ số của nó tỉ lệ với 1,2,3
gọi 3 chữ số của số cần tìm là a,b,c ( a,b,c \(\in\)N ; a\(\ne\)0, a,b,c, \(\le\)9 )
Theo đầu bài ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)\(\Rightarrow\frac{a}{1}=\frac{a+b+c}{1+2+3}\)\(\Rightarrow a=\frac{a+b+c}{6}\)
Do vậy : a + b + c \(⋮\)6 ( 1 )
Mặt khác số đó chia hết cho 18 nên số đó chia hết cho 9 \(\Rightarrow\)a + b + c \(⋮\)9 ( 2 )
Mà 0 < a + b + c \(\le\)27 ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) \(\Rightarrow\)a + b + c \(⋮\)18
Ta có : \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=3\)\(\Rightarrow a=3,b=6,c=9\)
\(\Rightarrow\)số đó là 396 hoặc 936
Đúng 0
Bình luận (0)
Tìm số tự nhiên có ba chữ số biết rằng số đó là bội của 18 và các chữ số của nó tỉ lệ với 1;2;3
A. 396
B. 936
C. 396 và 936
D. 369
Gọi ba chữ số của số phải tìm là a, b, c
![]()
Số phải tìm là bội của 18 nên số đó chia hết cho 9 , do đó a + b + c= 9 hoặc a + b + c = 18 hoặc a + b + c =27
Theo đề bài, các chữ số của số đó tỉ lệ với 1;2;3 nên
a 1 = b 2 = c 3
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
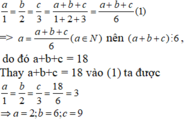
Lại có số phải tìm là bội của 18 nên chữ số hàng đơn vị của nó là số chẵn, do đó có hai số thỏa mãn đề bài là 396;936
Đáp án cần chọn là C
Đúng 0
Bình luận (0)
tìm số tự nhiên có 3 chữ số biết rằng số đó là bội của 18 và các chữ số của nó lần lượt tỉ lệ với 1:2:3
Gọi a, b,c lần lượt tỉ lệ với 1,2,3
a/1=b/2=c/3 và a+b+c=18
Áp dụng tính chất dãy tiwr số bằng :
a/1=b/2=c/3=a+b+c/1+2+3=18/6=3
Suy ra :a/1=3=>a=3
b/2=3=>b=6
c/3=3=>c=9
Đúng 0
Bình luận (0)
Gọi a , b , c là các chữ số của số có 3 chữ số cần tìm .Vì mỗi số a,b,c ko vượt quá 9 và a,b,c cũng ko thể đồng thời =0 , vì khi đó ta ko được số có 3 chữ số nên 1 <a+b+c<27
Mặt khác số phải tìm là bội của 18 nên a+b+c=9 hoặc a+b+c=18
Theo bài ra ta có :a/1=b/2=c/3=a+b+c/6
Do đó a+b+c chia hết cho 6
N ên a+b+c=18
=>a/1=b/2=c/3=18/6=3
=>a=3,b=6,c=9
Vì số phải tìm chia hết cho 18 nên số ở hàng dơn vị phải là số chẵn
Vậy các số cần phải tìm là 396;936
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm số tự nhiên có 3 chữ số biết rằng số đó là bội của 18 và các chữ số của nó lần lượt tỉ lệ với 1:2:3
Gọi các chữ số cần tìm là a;b;c
Vì a:b:c tỉ lệ vs 1:2:3 => \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)= \(\frac{18}{6}=3\)
=> a=3
b=6
c=9
Vì x là bội của 18 nên số cần tìm là 396 và 936
Đúng 0
Bình luận (3)
Tìm số tự nhiên có 3 chữ số, biết số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1;2;3
Do số cần tìm chia hết cho18 nên nó chia hết cho 2 và 9
=> chữ số tận cùng của số đó là số chẵn và tổng các chữ số của số đó chia hết cho 9
Do các chữ số tỷ lệ theo 1:2:3 thì có các bộ là (1; 2; 3), (2; 4; 6), (3; 6; 9)
Tổng các chữ số chia hết cho 9 thì chỉ có bộ (3; 6; 9) thỏa mãn
Do chữ số cuối cùng là chẵn nên chữ số hàng đơn vị là 6
Số cần tìm là 936 hoặc 396
Đúng 0
Bình luận (0)
gọi 3 chữ số của số cần tìm là a;b;c.theo bài ra ta có:
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{a+b+c}{6}\)
số cần tìm chia hết cho 18=>tổng các chữ số chia hết 9;6
=>tổng các chữ số chia hết cho 9;2
=>a+b+c chia hết cho 18
a+b+c<(=)27
=>a+b+c=18
\(\Rightarrow\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{18}{6}=3\)
=>a=3;b=6;c=9
=>số cần tìm là:396;936
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm số tự nhiên có 3 chữ số, biết số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1;2;3
Tìm số tự nhiên có 3 chữ số, biết đó là bội của 18 và các chữ số của nó tỉ lệ 1 ÷ 2 ÷3
Gọi x là số cần tìm và a,b,c là lần lượt các số của nó ( x thuộc N* )
x chia hết cho 18 suy ra x chia hết cho 2 vậy x chẵn
Ta có a,b,c tỉ lệ với 1:2:3 thì nhân theo hệ quả ta được các số : 123, 246, 369
Mà x chia hết cho 9 suy ra x chia hết cho 3
Thỏa mãn điều kiện trên ta được các số 396 và 936
Vì x chia hết cho 18 suy ra x = 936
==> x = 936
tìm số tự nhiên có 3 chữ số, biết số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1:2:3
Không có số nào cả. Thử với :123;246;369 đều không chia hết cho 18 còn 4812 thì có 4 chữ số nên ko thỏa mãn
Đúng 0
Bình luận (0)
Do số cần tìm chia hết cho18 nên nó chia hết cho 2 và 9
=> chữ số tận cùng của số đó là số chẵn và tổng các chữ số của số đó chia hết cho 9
Do các chữ số tỷ lệ theo 1:2:3 thì có các bộ là (1; 2; 3), (2; 4; 6), (3; 6; 9)
Tổng các chữ số chia hết cho 9 thì chỉ có bộ (3; 6; 9) thỏa mãn
Do chữ số cuối cùng là chẵn nên chữ số hàng đơn vị là 6
Số cần tìm là 936 hoặc 396
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
TÌm số tự nhiên có 3 chữ số, biết số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1:2:3.
Gọi chữ số nhỏ nhất là x
=> Ba chữ số theo tỉ lệ là: x, 2x, 3x với 3x ≤ 9
=> x ≤ 3 (1)
Vì số cần tìm chia hết cho 18, nghĩa là chia hết cho 9
Nên (x + 2x + 3x) = 6x chia hết cho 9
=> x chia hết cho 3 (2)
Từ (1) & (2), suy ra: x = 3
=> Ba chữ số là 3, 6, 9
Theo đề bài số cần tìm chia hết cho 18 (18 là số chẵn), nghĩa là chia hết cho 2, vậy chữ số cuối phải là 6
=> Số cần tìm là 396 hoặc 936
Ai k mk mk k lại!
Đúng 1
Bình luận (0)
Gọi x là số cần tìm và a,b,c lần lượt là các số của chúng (x \(\in\)N*)
Nếu x chia hết cho 18 thì x chia hết cho 2, x chẵn
Ta có: a,b,c tỉ lệ với 1,2,3 thì nhân theo hệ quả ta được các số 123;246;369
x chia hết cho 18 thì x chia hết cho 9 => x chia hết cho 3
Thỏa mãn các điều kiện trên ta được các số 396 và 936
Vậy số cần tìm là 396 và 936
Đúng 0
Bình luận (0)
Gọi x là số cần tìm và a,b,c lần lượt là các số của chúng (x \(∈\)N*)
Nếu x chia hết cho 18 thì x chia hết cho 2, x chẵn
Ta có: a,b,c tỉ lệ với 1,2,3 thì nhân theo hệ quả ta được các số 123;246;369
Vì x chia hết cho 18 nên x chia hết cho 9 => x chia hết cho 3
Thỏa mãn các điều kiện trên ta được các số 396 và 936
Vậy số cần tìm là 396 và 936
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

























