Cho 2 điểm AB thuộc nửa mặt phẳng đối nhau bờ xy.(AB # xy).Đoạn thẳng AB cắt xy tại m.
â,Cho biết góc \(\widehat{AMY}\)=150.Hãy tính số đo góc\(\widehat{AMX}\)va \(\widehat{BMY}\)
b,Trên tia Mx lấy một điểm O, gia su AOB =60
Bài 3. Cho AABC. Gọi K là trung điểm của BC. Kẻ AM 1 AC và AM = AC, kẻ AN 1 AB và AN = AB (M và B thuộc hai nửa mặt phẳng đối nhau bờ AC, N và C thuộc hai nửa mặt phẳng đối nhau bờ AB). Trên tia AK lấy điểm P sao cho K là trung điểm của AP. Chứng minh:
а) AC // ВР
b) BM = CN
с) ДАВР = ANAM
d) AK L MN.
a: Xét ΔKAC và ΔKPB có
KA=KP
\(\widehat{AKC}=\widehat{PKB}\)
KC=KB
Do đó:ΔKAC=ΔKPB
=>\(\widehat{KAC}=\widehat{KPB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//PB
b: \(\widehat{NAC}=\widehat{NAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BAM}=\widehat{BAC}+\widehat{MAC}=90^0+\widehat{BAC}\)
Do đó: \(\widehat{BAM}=\widehat{NAC}\)
Xét ΔBAM và ΔNAC có
BA=NA
\(\widehat{BAM}=\widehat{NAC}\)
AM=AC
Do đó: ΔBAM=ΔNAC
=>BM=CN
c:
ΔKBP=ΔKCA
=>BP=AC
mà AC=AM
nên BP=AM
AC//BP
=>\(\widehat{ABP}+\widehat{BAC}=180^0\)(1)
\(\widehat{BAC}+\widehat{NAM}+\widehat{NAB}+\widehat{MAC}=360^0\)
=>\(\widehat{BAC}+\widehat{NAM}+90^0+90^0=360^0\)
=>\(\widehat{NAM}+\widehat{BAC}=180^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ABP}=\widehat{NAM}\)
Xét ΔABP và ΔNAM có
AB=NA
\(\widehat{ABP}=\widehat{NAM}\)
BP=AM
Do đó: ΔABP=ΔNAM
Cho 2 nửa mặt phẳng đối nhau chung bờ d. Trên 1 nữa mặt phẳng bờ d lấy điểm A. Trên 1 nửa mặt phẳng bờ d không chứa a, lấy điểm B. Trên nửa mặt phẳng bờ d lấy điểm C. Xác định điểm D thuộc d sao cho A, C, D thẳng hàng. Nối tia AB, BC, CA . Hỏi 3 tia AB, BC, CA cắt nhau tạo thành mấy góc? Kể tên các góc đó?
cho 2 điểm A,B thuộc 2 nửa mặt phẳng đối nhau bờ xy(A,B không thuộc đường thẳng xy).Đoạn thẳng AB cắt đường thẳng xy tại M.lấy điển O thuộc xy sao cho tia Ox nằm giữa tia OA,OB,kể tên các góc bẹt có trong hình
Cho tam giác ABC ( góc A < 90 độ ) . TẠi A kẻ Ã vuông góc với AC , M thuộc Ax sao cho AM=AC . M,B thuộc 2 nửa mặt phẳng đối nhau bờ AC . Tại A kẻ Ay vuông góc với AB , n thuộc Ay sao cho AN = AB ( N,C thuộc 2 nửa mặt phẳng đối nhau bờ AB ) a) chứng minh tam giác ABM = tam giác ANC b) BM=CN c) Bm vuông gó
a) Ta có: \(\widehat{MAB}=\widehat{BAC}+\widehat{CAM}=\widehat{BAC}+90^o\left(AM\perp AC\right).\)
\(\widehat{CAN}=\widehat{BAC}+\widehat{BAN}=\widehat{BAC}+90^o\left(AN\perp AB\right).\)
\(\Rightarrow\widehat{MAB}=\widehat{CAN}.\)
Xét tam giác ABM và tam giác ANC:
\(\widehat{MAB}=\widehat{CAN}\left(cmt\right).\)
AB = AB (gt).
AM = AC (gt).
\(\Rightarrow\) Tam giác ABM = Tam giác ANC (c - g - c).
b) Tam giác ABM = Tam giác ANC (cmt).
\(\Rightarrow\) BM = NC (2 cạnh tương ứng).
Câu a: cho 2 điểm A và B thuộc 2 nửa mặt phẳng đối nhau bờ là đoạn thẳng xy . Đoạn thẳng AB cắt xy tại M . Cho biết góc AMY = 150 độ . Tính góc AMX , BMY
Câu b : trên tia Mx láy điểm O . Nếu AOB = 60 độ , AOY=40 độ . Tính BOX
Cho tam giác ABC. K là trung điểm của BC.
AM vuông góc với AC và AM = AC; AN vuông góc với AB và AN = AB (M và B thuộc 2 nửa mặt phẳng đối nhau bờ AC; N và C thuộc 2 nửa mặt phẳng đối nhau bờ AB)
Trên tia AK lấy điểm P sao cho K là trung điểm của AP.
Chứng minh:
a, AC // BP
b, Tam giác ABP = tam giác NAM
c, AK vuông góc với MN
a) Xet tam giac BKP va tam giac AKC ta co
AK=KP ( K la trung diem AP)
BK=KC( K la trung diem BC)
goc AKB= goc PKC ( 2 goc doi dinh)
--> tam giac BKP= tam giac AKC ( c-g-c)
--> goc KBP=goc KCA ( 2 goc tuong ung)
ma 2 goc nam o vi tri so le trong nen AC//BP
b) ta co:
goc NAM + goc BAC + goc MAC+ goc NAB=360
goc NAM + goc BAC +90 +90 =360
goc NAM + goc BAC =180
ma goc ABP + goc BAC =180 ( 2 goc trong cung phia va AC//BP)
nen goc NAM = goc ABP
ta co : AC= BP ( tam giac AKC = tam giac BKP)
AC = AM (gt)
--> BP =AM
Xet tam giac NAM va tam giac ABP ta co
goc NAM = goc ABP (cmt)
AN= AB( gt)
AM= BP (cmt)
--> tam giac NAM = tam giac ABP (c-g-c)
c) Keo dai KA cat NM tai H
ta co
goc HMA= goc APB ( tam giac NAM = tam giac ABP)
goc APB= goc PAC ( 2 goc so le trong va AC//BP)
---> goc HMA = goc APB
ta co:
goc HAM+ goc MAC+ goc CAP=180
goc HAM + 90 + goc CAP=180
goc HAM+ goc CAP =90
ma goc CAP = goc AMH ( cmt)
nen goc HAM+ goc AMH =90
Xet tam giac HAM ta co
goc HAM+ goc AMH + goc AHM =180 ( tong 3 goc trong tam giac )
90+ goc AHM=180
goc AHM =90
--> AK vuong goc MN tai H
Cho tam giác ABC ( góc A < 90 độ ) . Tại A kẻ Ax vuông góc với AC trên Ax lấy điểm M sao cho AM=AC ( M,B thuộc 2 nửa mặt phẳng đối nhau bờ có chứa tia AC ). Tại A kẻ Ay vuông góc với AB , trên Ax lấy điểm N sao cho AN = AB ( N và C thuộc 2 nửa mặt phẳng đối nhau bờ có chứa tia AB ). Chứng minh:
a) Tam giác ABM = tam giác ANC
b) BM=CN
c) BM vuông góc với CN
Cho đường thẳng xy và hai điểm M, N thuộc hai nửa mặt phẳng đối nhau bờ xy (M, N không thuộc xy). Nêu cách lấy điểm O thuộc xy sao cho: Tia Ox nằm giữa hai tia OM và ON.
Vẽ đoạn thẳng MN cắt xy tại C
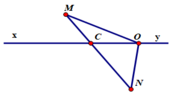
Lấy điểm O thuộc tia Cy thì tia Ox nằm giữa hai tia OM, ON
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.
a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.
b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
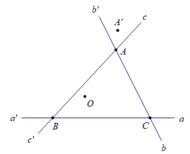
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.