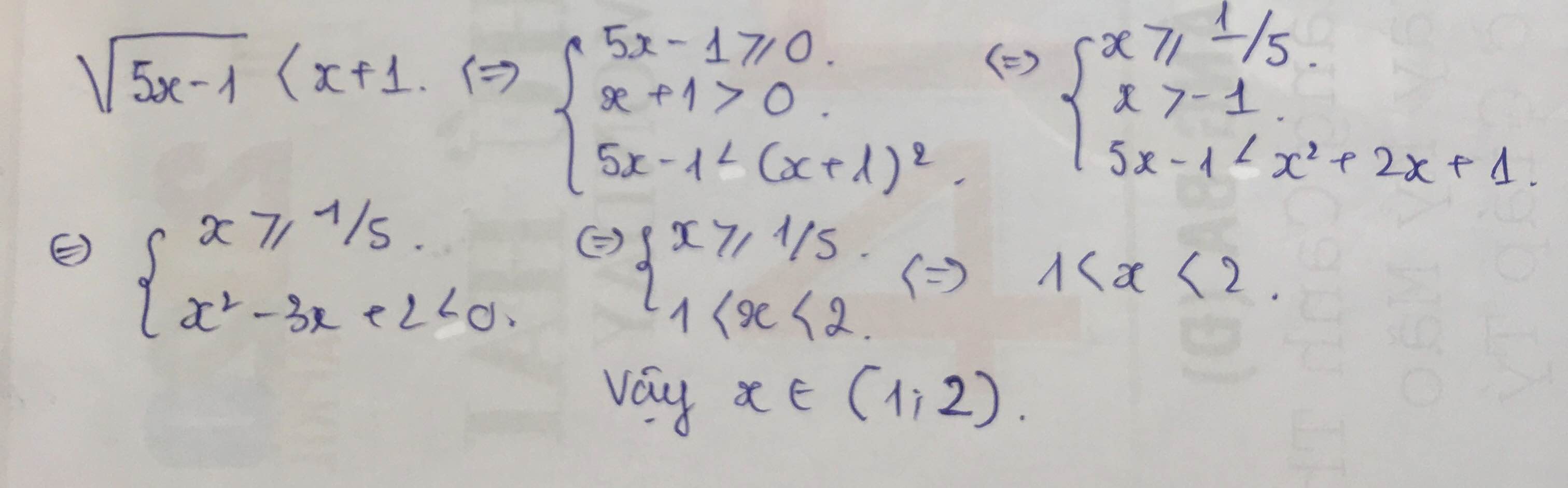a: \(3+\sqrt{2x-3}=x\)

=>\(\sqrt{2x-3}=x-3\)

=>x>=3 và 2x-3=(x-3)^2

=>x>=3 và x^2-6x+9=2x-3

=>x>=3 và x^2-8x+12=0

=>x>=3 và (x-2)(x-6)=0

=>x>=3 và \(x\in\left\{2;6\right\}\)

=>x=6

b: \(\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)-2x=-4\)

=>\(2x-3\sqrt{x}+2\sqrt{x}-3-2x=-4\)

=>\(-\sqrt{x}-3=-4\)

=>\(-\sqrt{x}=-1\)

=>căn x=1

=>x=1(nhận)

c: \(\sqrt{2x+1}-x+1=0\)

=>\(\sqrt{2x+1}=x-1\)

=>x>=1 và (x-1)^2=2x+1

=>x>=1 và x^2-2x+1=2x+1

=>x>=1 và x^2-4x=0

=>x(x-4)=0 và x>=1

=>x=4

Đầu tiên ta đặt dk 2x^2 - 2x >=0 <=> x<=0 và x>=1 
x^4 -2x^3+x - căn(2x^2-2x)=0 
<=> x(x^3-2x^2+1) - căn[2x(x-1)]=0 
<=>x[(x^3-x^2)-(x^2-1)] - căn[2x(x-1)]=0 
<=>x[x^2(x-1)-(x-1)(x+1)] - căn[2x(x-1)]=0 
<=>x(x-1)(x^2-x-1) - căn[2x(x-1)]=0 
<=>x(x-1)[x(x-1)-1] - căn[2x(x-1)]=0 
<=>[x(x-1)]^2 -x(x-1) - căn[2x(x-1)]=0(*) 
Nhân cả hai vế của pt(*) cho 4 ta được: 
4[x(x-1)]^2 -4x(x-1) - 4căn[2x(x-1)]=0(**) 
Đến đây ta đặt t=căn[2x(x-1)] điều kiện t>=0 ta được pt sau 
t^4 -2t^2 -4t =0 
<=> t(t^3 - 2t -4)=0 
<=> t=0 hoặc t^3-2t -4=0 
với t=0 thế vào t= căn[2x(x-1)]=0 => x=0 hoặc x=1 
với t^3-2t-4=0 ta thấy pt này có một nghiệm t=2 
<=> (t-2)(t^2+2t+2)=0(ở đây ta thực hiện chia t^3-2t-4 cho t-2) 
<=>t=2 
thế t=2 vào t=căn[2x(x-1)]=2 ta tìm được x=-1 hoặc x=2 
thỏa mãn dk x<=0 và x>=1 
Vậy pt đã cho có các nghiệm sau x=0; x=1; x=-1; x=2 
Kết luận: x=0; x=1; x=-1; x=2

Em trục căn thức:

\(\sqrt{x+3}-2\sqrt{x}=\sqrt{2x+2}-\sqrt{3x+1}\)

<=> \(\frac{-3x+3}{\sqrt{x+3}+2\sqrt{x}}=\frac{-x+1}{\sqrt{2x+2}+\sqrt{3x+1}}\)

=> nhân tử chung là -x + 1 . Tự làm tiếp nhé!

làm như cô thì vẫn cần phải đánh giá rất khó chịu nhé

\(\sqrt{x+3}-2\sqrt{x}=\sqrt{2x+2}-\sqrt{3x+1}\left(ĐKXĐ:x\ge0\right)\)

\(< =>\sqrt{x+3}-\sqrt{2x+2}+\sqrt{3x+1}-2\sqrt{x}=0\)

\(< =>\frac{\sqrt{x+3}^2-\sqrt{2x+2}^2}{\sqrt{x+3}+\sqrt{2x+2}}+\frac{\sqrt{3x+1}^2-4\sqrt{x}^2}{\sqrt{3x+1}+2\sqrt{x}}=0\)

\(< =>\frac{x+3-2x-2}{\sqrt{x+3}+\sqrt{2x+2}}+\frac{3x+1-4x}{\sqrt{3x+1}+2\sqrt{x}}=0\)

\(< =>\frac{1-x}{\sqrt{x+3}+\sqrt{2x+2}}+\frac{1-x}{\sqrt{3x+1}+2\sqrt{x}}=0\)

\(< =>\left(1-x\right)\left(\frac{1}{\sqrt{x+3}+\sqrt{2x+2}}+\frac{1}{\sqrt{3x+1}+2\sqrt{x}}\right)=0< =>x=1\)

\(ĐK:x\ge2\)

\(\sqrt{x+1}=\sqrt{x-2}+1\)

\(\Leftrightarrow x+1=x-1+2\sqrt{x-2}\)

\(\Leftrightarrow2\sqrt{x-2}=2\Leftrightarrow x=3\)