\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\)

\(\Rightarrow\frac{x}{6}-\frac{1}{2}=\frac{1}{y}\)

\(\Rightarrow\frac{x}{6}-\frac{3}{6}=\frac{1}{y}\)

\(\Rightarrow\frac{x-3}{6}=\frac{1}{y}\)

\(\Rightarrow\left(x-3\right)y=6\)

Ta có bảng sau:

...

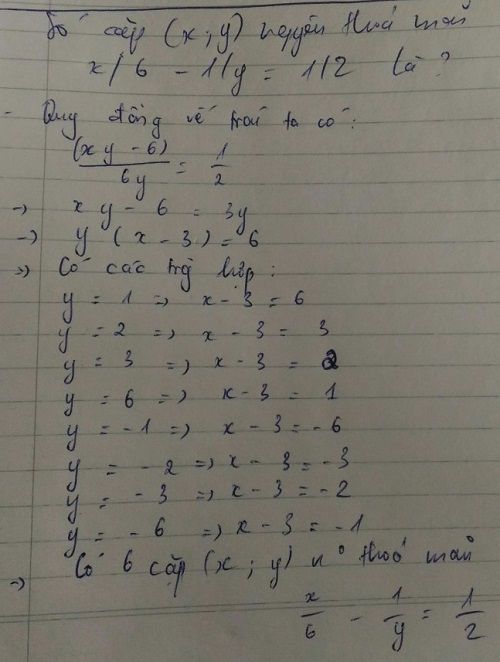
Bạn lấy bài này làm mẫu của anh mình nhé !!!

Bài này bạn đăng rồi Nguyễn Nhật Minh trả lời đúng rồi mà :

http://olm.vn/hoi-dap/question/314450.html

\(\frac{5}{x}=\frac{1}{8}-\frac{y}{4}=\frac{1-2y}{8}\)

\(\Rightarrow x=5:\frac{1-2y}{8}=\frac{40}{1-2y}\)

Do x, y là số nguyên => 40 chia hết cho 1  - 2y 

=> 1 - 2y thuộc Ư(40)

Mà 1 - 2y là lẻ => 1 - 2y thuộc {-1; 1; -5; 5}

=> y thuộc {1; 0; 3; -2}

=> x thuộc {-40; 40; -8; 8}

ko biết làm hihi

1)

\(xy-y=x\Leftrightarrow y=\frac{x}{x-1}=1+\frac{1}{x-1}\)

y thuộc Z => x -1 thuộc U(1) ={ -1;1}

+x =-1 => y =0

+x =1 => y =2

2) \(x.\left(1-\frac{1}{7}\right)<1\frac{6}{7}\Leftrightarrow x.\frac{6}{7}<\frac{13}{7}\Rightarrow x<\frac{13}{7}.\frac{7}{6}=\frac{13}{6}=2,1\left(6\right)\)

x thuộc Z⁺ => x thuộc {1;2}

khỉ gió khó quá

Ê cu tao đây này

k cho tớ đi tớ giải cho kết quả là

1/x =2 - 1/y=(2y-1)/y

=> x= y/(2y-1)

=> 2x=(2y-1+1)/(2y-1)=1 + 1/(2y-1)

Để x nguyên thì 1 chia hết cho 2y-1

2y-1=±1

+/ 2y-1=-1 => y=0 => x=0

+/ 2y-1=1 => y=1;  x=2

Có 2 cặp x, y thỏa mãn: (0; 0); (2; 1)