Cho tam giác ABC, M là trung điểm cạnh BC. cmr:
\(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\)
Cho tam giác ABC, M là trung điểm cạnh BC. C/m \(\frac{AB+AC-BC}{2}
Cho \(M,N\) lần lượt là trung điểm của hai cạnh \(AB;AC\) của tam giác \(ABC\).
a) Tính các tỉ số \(\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}\);
b) Chứng mình \(MN//BC\);
c) Chứng minh \(\frac{{MN}}{{BC}} = \frac{1}{2}\).
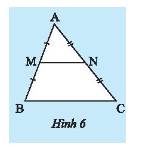
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).
Cho tam giác ABC,Gọi M là trung điểm của BC
CMR:\(AM< \frac{AB+AC}{2}\)
Trên tia đối của tia AM lấy điểm D sao cho AM=MD
Xét tam giác AMB VÀ TAM GIÁC DMC có
MB=MC(gt)
AM=MD(cách dựng)
\(\widehat{AMB}=\widehat{DMC}\)(ĐÓI ĐỈNH)
\(\Rightarrow\)Tam giác AMB=Tam giác BMC(c-g-c)
\(\Rightarrow\)AB=CD(2 cạnh tương ứng)
Xét tam giác ACD có
AD<CD+AC(bất đẳng thức tam giác)
\(\Rightarrow\)AD<AB+AC(VÌ AB=CD)
Mà AD=AM+MD=2AM
\(\Rightarrow2AM< AB+AC\)
\(\Rightarrow AM< \frac{AB+AC}{2}\)(ĐPCM)
Kẻ đoạn thẳng AM
Trên tia AM lấy điểm K sao cho M là trung điểm của AK
=> MA = MK = AK/2 => 2AM = AK
M là trung điểm của BC ( gt ) => MB = MC
Xét tam giác AMB và tam giác KMC có :
MA = MK ( cmt )
AMB = KMC ( đối đỉnh )
MB = MC ( cmt )
Do đó tam giác AMB = tam giác KMC ( c . g . c )
=> AB = CK ( 2 cạnh tương ứng )
CÓ AK < AC + CK ( bất đẳng thức trong tam giác )
hay 2AM < AC + AB
=> AM < \(\frac{AC+AB}{2}\)( dpcm )
Vậy ...
Sửa đề \(AM< \frac{AB+AC+BC}{2}\)
Có AM<AB+BM(BĐT tam giác)
AM<AC+MC(BĐT tam giác)
=> 2AM<AB+AC+BM+MC=AB+AC+BC
Cho M là một điểm của tam giác ABC .CMR : \(\frac{AB+AC+BC}{2}\)<AM+BM+CM<AB+AC+BC
Cho tam giác ABC, \(\widehat{B}=120^o\), BC= 16cm, AB= 8cm, AC= 21cm. Phân giác góc B cắt AC tại D. Gọi M là trung điểm BC. AM cắt BC tại I, K là hình chiếu của I trên BC. CMR: \(\frac{1}{4.IK^2}=\frac{1}{AB^2}+\frac{1}{AM^2}\).
Cho tam giác ABC. M là trung điểm của BC. CMR AB2 + AC2 = \(\frac{BC^2}{2}+2.AM^2\)
cho tam giác ABC có AB<AC .Gọi M là trung điểm của cạnh BC
CMR :\(\dfrac{AC-AB}{2}\)< AM <\(\dfrac{AB+AC}{2}\)\
GỢI Ý :Lấy điểm D trên tia đối MA sao cho MD=MA
Cho tam giac abc gọi M là trung điểm của cạnh bc. Cmr (ab+ac-bc)/2<am<(ab+ac)/2
Áp dụng bất đẳng thức tam giác với hai tam giác AMB và AMC ,ta lần lượt có :
AM > AB - BM
AM > AC - MC
Cộng theo từng vế hai bất đẳng thức trên,ta có :
2AM > AB + AC - (BM + MC) = AB + AC - BC hay \(AM>\frac{AB+AC-BC}{2}\) (1)
Trên tia đối của tia MA lấy điểm D sao cho MD = MA
Xét \(\Delta AMB\)và \(\Delta DMC\)có :
AM = DM(gt)
MB = MC(gt)
\(\widehat{M}\)chung
=> \(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
=> \(\widehat{MAB}=\widehat{MDC}\)(hai góc tương ứng)
=> CD = AB(hai cạnh tương ứng)
Xét \(\Delta ACD\),theo bất đẳng thức tam giác ta có :
AD < AC + CD
=> \(2AM< AC+AB\)
=> \(AM< \frac{AB+AC}{2}\)(2)
Từ (1) và (2) suy ra \(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\)
Cho tam giác ABC có AB = c ; AC = b . Gọi M là trung điểm của BC. CMR : \(AM< \frac{b+c}{2}\)
Trên tia đối của tia MA lấy điểm D sao cho MD=MA
Xét \(\Delta AMB\)và \(\Delta DMC\):
MB=MC(gt)
\(\widehat{AMB}=\widehat{DMC}\)(đối đỉnh)
BM=CM(gt)
=> \(\Delta AMB=\Delta DMC\left(c.-g-c\right)\)
=> DC=AB=c
Xét \(\Delta ACD\)có: AD<AC+DC
=> 2AM<b+c
=> \(AM< \frac{b+c}{2}\)
=> Đpcm
P/s:Phần này là phần BĐT tam giác ý, dễ mà:>