tìm nghiệm nguyên của pt
x3y3−x3=91
tìm nghiệm nguyên của phương trình : x3 - x2y + 3x -2y - 5 = 0
Lời giải:
PT $\Leftrightarrow x^3+3x-5=x^2y+2y=y(x^2+2)$
$\Rightarrow y=\frac{x^3+3x-5}{x^2+2}$
Để $y$ nguyên thì $x^3+3x-5\vdots x^2+2$
$\Leftrightarrow x(x^2+2)+x-5\vdots x^2+2$
$\Leftrightarrow x-5\vdots x^2+2(1)$
$\Rightarrow x^2-5x\vdots x^2+2$
$\Leftrightarrow x^2+2-(5x+2)\vdots x^2+2$
$\Leftrightarrow 5x+2\vdots x^2+2(2)$
Từ $(1);(2)\Rightarrow 5(x-5)-(5x+2)\vdots x^2+2$
$\Leftrightarrow 27\vdots x^2+2$. Do $x^2+2\geq 2$ nên:
$\Rightarrow x^2+2\in\left\{3;9;27\right\}$
$\Rightarrow x^2\in\left\{1;7;25\right\}$
Do $x$ nguyên nên $x\in\left\{\pm 1; \pm 5\right\}$
Thay vào $y$ ta tìm được:
$x=-1\Rightarrow y=-3$
$x=5\Rightarrow y=5$
Hãy tìm nghiệm nguyên của bất phương trình sau: x(x3 - x + 6) > 9
Ta có: x(x3 - x + 6) > 9
⇔ x4 - x2 + 6x - 9 > 0
⇔ f(x) > 0
thấy f(x) > 0 khi
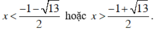
Vậy tập nghiệm của bất phương trình là
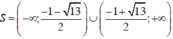
Tìm nghiệm nguyên của pt: x3 - y3 = 91
x3 - y3 = 91
<=>(x-y)(x2+xy+y2)=91
Do x-y < x2+xy+y2 và x2+xy+y2>0 nên ta có 2 trường hợp:
Th1: \(\hept{\begin{cases}x-y=1\\x^2+xy+y^2=91\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1+y\\\left(1+y\right)^2+\left(1+y\right).y+y^2=91\end{cases}}\)
=>1+2y+y2+y+y2+y2=91
<=>3y2+3y-90=0
<=>y1=5;y2=-6 (nhận 2 nghiệm)
Với y=5 => x=6 (nhận)
Với y=-6 =>x=-5 (nhận)
Th2: \(\hept{\begin{cases}x-y=7\\x^2+xy+y^2=13\end{cases}}\Leftrightarrow\hept{\begin{cases}x=7+y\\\left(7+y\right)^2+\left(7+y\right).y+y^2=13\end{cases}}\)
=>49+14y+y2+7y+y2+y2=13
<=>3y2+21y+36=0
<=>y3=-3;y4=-4 (nhận 2 nghiệm )
Với y=-3 =>x=4
Với y=-4 =>x=3
Vậy (x;y)= (6;5) ;(-5;-6);(4;-3);(3;-4)
sửa xíu giúp mik là do x-y < hoặc = x2+xy+y2 .........
Tìm tất cả các nghiệm nguyên x, y của phương trình x3 + 2x2 + 3x + 2 = y3.
+, Nếu x = 0 => ko tồn tại y thuộc Z
+, Nếu x khác 0 => x^2 >= 1 => x^2-1 >= 0
Có : y^3 = x^3+2x^2+3x+2 > x^3 ( vì 2x^2+3x+2 > 0 )
Lại có : y^3 = (x^3+3x^3+3x+1)-(x^2-1) = (x+1)^3 - (x^2-1) < = (x+1)^3
=> x^3 < y^3 < = (x+1)^3
=> y^3 = (x+1)^3
=> x^2-1 = 0
=> x=-1 hoặc x=1
+, Với x=-1 thì y = 0
+, Với x=1 thì y = 2
Vậy .............
Tk mk nha
Ta có: \(x^3+2x^2+3x+2=y^3\) (1)
Xét \(2x^2+3x+2=2\left(x^2+\frac{3}{2}x\right)+2=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+2-2.\frac{9}{16}\)
\(=2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\) Vì \(\left(x+\frac{3}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\ge\frac{7}{8}>0\)
\(\Rightarrow y^3>x^3\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2\ge\left(x+1\right)^3\) \(\Rightarrow x^3+2x^2+3x+2\ge x^3+3x^2+3x+1\)
\(\Rightarrow x^3+3x^2+3x+1-x^3-2x^2-3x-2\le0\)
\(\Rightarrow x^2-1\le0\Rightarrow x^2\le1\) Vì \(x\in Z\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=0\end{cases}}\)
+ TH1: x2 = 0 => x =0 Thay vào pt (1) ta được y3 = 2 (loại) vì y nguyên
+ TH2 : x2 = 1 => \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Thay x=1 vào pt (1) ta đc: 1+2+3+2 = 8 = y3 => y = 2
Thay x= -1 vào pt (1) ta đc: -1 + 2 -3 +2 = 0 =y3 => y = 0
Vậy cặp (x;y) là (1;2) ; (-1;0).
\(Xét \(2x^2+3x+2=2\left(x+\dfrac{3}{4}\right)^2+\dfrac{7}{16}>0\forall x\in R\) => \(x^3< y^3\left(1\right)\) (1) Giả sử : \(y^3< \left(x+2\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2< x^3+6x^2+12x+8\) \(\Leftrightarrow-4x^2-9x-6< 0\) \(\Leftrightarrow4x^2+9x+6>0\) \(\Leftrightarrow4\left(x+\dfrac{9}{8}\right)^2+\dfrac{15}{64}>0\) => Giả sử đúng . => \(y^3< \left(x+2\right)^3\left(2\right)\) Từ (1)(2) => \(y^3=\left(x+1\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2=x^3+3x^2+3x+1\) \(\Leftrightarrow x^2=1\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\) .) Khi \(x=1\Rightarrow y=2\). .) Khi \(x=-1\Rightarrow y=0\) Vậy nghiệm của pt ( x;y ) = {( 1;2 ) ; ( -1;0 )}\)
1) Tìm nghiệm nguyên của phương trình : x2= 2y2+2013
2) Giải phương trình x3+2x2- 4x +\(\dfrac{8}{3}\)=0
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
Tìm nghiệm nguyên
x^2+91=y^2
\(Ta\) \(có :\)\(x^2+91=y^2\)
\(\Rightarrow\)\(x^2 - y^2 = - 91\)
\(\Rightarrow\)\(( x - y)(x +y)=-91\)
\(Ta\) \(Lập\) \(Bảng :\)
| \(x - y\) | \(-1\) | \(-91\) | \(7\) | \(13\) |
| \(x +y\) | \(91\) | \(1\) | \(-13\) | \(- 7\) |
| \(x\) | \(45\) | \(-45\) | \(- 3\) | \(3\) |
| \(y\) | \(46\) | \(46\) | \(- 10\) | \(-10\) |
\(Vậy :..............\)
Tìm nghiệm nguyên: \(x^3+y^3=91\)
Tìm nghiệm nguyên: \(x^3+y^3=91\)
1)Tìm nghiệm nguyên của phương trình:
y3-x3=91
2)Tìm nghiệm nguyên của phương trình:
x2=y2+y+13
3)Tìm nghiệm nguyên của phương trình:
x2+x+1991=y2