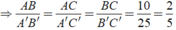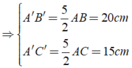cho tam giác ABC = tam giác A'B'C'. Biết góc BC = 10cm; góc AB : góc AC = 4 : 3 và góc AB + góc AC = 14cm. Tính các cạnh của tam giác A'B'C'

Những câu hỏi liên quan
Cho tam giác ABC đồng dạng với tam giác A'B'C'. Cho biết AB = 6cm, BC = 10cm, AC = 14cm và chu vi tam giác A'B'C' bằng 45cm. Hãy tính độ dài các cạnh của tam giác A'B'C'
Ta có:
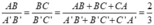
Từ đó tính được A'B' = 9cm, B'C' = 15cm, A'C' = 21cm
Đúng 0
Bình luận (0)
Cho tam giác ABC đồng dạng với tam giác ABC . Cho biết
A
B
16
,
2
c
m
,
B
C
24
,
3
c
m
,
C
A
32
,
4
c
m
, hãy tính độ dài các cạnh của tam giác ABC nếu:a) AB lớn hơn AB là 10cm;b) AB lớn hơn AB là 10c...
Đọc tiếp
Cho tam giác ABC đồng dạng với tam giác A'B'C' . Cho biết A B = 16 , 2 c m , B C = 24 , 3 c m , C A = 32 , 4 c m , hãy tính độ dài các cạnh của tam giác A'B'C' nếu:
a) AB lớn hơn A'B' là 10cm;
b) A'B' lớn hơn AB là 10cm
Ta có
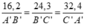
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm
Đúng 0
Bình luận (0)
1 Cho tam giác ABC và tam giác A'B'C' có góc A = góc A' BC = B'C' góc B = B' chứng minh rằng tam giác ABC = tam giác A'B'C'
2 Cho tam giác ABC có AB = AC phân giác AD chứng minh rằng AD vuông góc với BC
AI TRA LỜI NHANH GIÚP MÌNH VỚI TvT
2. \(\Delta ABC\)có AB=AC \(\Rightarrow\Delta ABC\)cân.
AD là phân giác \(\Delta ABC\)mà \(\Delta ABC\)cân.
\(\Rightarrow AD\)l là đường trung trực \(\Delta ABC\)..
\(\Rightarrow AD\)là đường cao \(\Delta ABC\)..
\(\Leftrightarrow AD\perp BC\).
Hình 1 :
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có : Góc A = Góc A' ( gt ); \(BC=B'C'\left(gt\right)\); Góc B = Góc B' ( gt )
\(\Rightarrow\Delta ABC=\Delta A'B'C\left(ch-gn\right)\)
Hình 2 :
Vì \(\Delta ABC\) có \(AB=AC\Leftrightarrow\Delta ABC\) cân tại A . Vì AD là phân giác góc A
\(\Leftrightarrow\) ^BAD = ^CAD. Xét \(\Delta ABD\) và \(\Delta ACD\) có : \(AB=AC\left(gt\right)\); ^BAD = ^CAD; AD chung.
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\Leftrightarrow\) ^ADB = ^ADC ( tương ứng ) . Mà ^ADB + ^ADC = 1800 ( kề bù )
\(\Leftrightarrow\) ^ADB = ^ADC = 1800 : 2 = 900 nên suy ra \(AD\perp BC\)
Xem thêm câu trả lời
Cho tam giác ABC và tg A'B'C', có góc B = góc B', góc C = góc C'. Vẽ AH vuông góc BC, A'H' vuông góc B'C' (H thuộc BC, H' thuộc B'C'). Biết AH =A'H'.Chứng minh tam giác ABC = tg A'B'C'.
Cho Δ ABC có AB = 8cm, AC = 6cm, BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Ta có: Δ ABC đồng dạng Δ A'B'C'
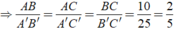
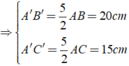
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 16,2cm, BC = 24,3cm, AC = 32,7cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng tam giác A'B'C đồng dạng với tam giác ABC và:
ΔABC đồng dạng với ΔA'B'C'
=>A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/162=B'C'/243=A'C'/327
=>A'B'/54=B'C'/81=A'C'/109
Đúng 0
Bình luận (0)
Cho tam giac ABC = tam giac A'B'C'.Gọi M là trung điểm của BC, M' là trung điểm của B'C'.Biết AM=A'M'.CMR :
a) tam giác ABC = tam giac A'B'C'
b) góc AMC= góc A'M'C'
cho tam giác ABC và A'B'C' có :góc A=A' ; AB= 3cm; A'B' = 3cm;AC= 4cm ; A'C' = 4cm
a) so sánh tam giác ABC và tam giác A'B'C'
b) Giả sử góc A = 90 .Tính BC
a) Làm theo bạn Doan Thanh phuong nhé!
b) Ta có: A = 90o => Tam giác ABC vuông tại a.
Áp dụng định lý Pitago. Ta có:
\(AB^2+AC^2=BC^2\Leftrightarrow3^2+4^2=9+16=25\)
\(\Rightarrow BC^2=25\). Mà \(25=5^2\Rightarrow BC=5\) cm
Đúng 0
Bình luận (0)
a) Xét tam giác ABC và tam giác A'B'C' có :
\(\widehat{A}=\widehat{A'}\left(gt\right)\)
AB = A'B' ( gt )
AC = A'C' ( gt )
Suy ra tam giác ABC = tam giác A'B'C' ( c - g - c )
b) Ta có tam giác ABC vuông tại A ( gt )
=> AB2 + AC2 = BC2 ( định lý Py-ta-go )
hay 32 + 42 = BC2
BC2 = 32 + 42 = 9 + 16 = 25
=> BC = 5
Đúng 0
Bình luận (0)
a) Xét tam giác ABC và tam giác A'B'C' có :
^A=^A'(gt)
AB = A'B' ( gt )
AC = A'C' ( gt )
Suy ra tam giác ABC = tam giác A'B'C' ( c - g - c )
b) Ta có tam giác ABC vuông tại A ( gt )
=> AB2 + AC2 = BC2 ( định lý Py-ta-go )
hay 32 + 42 = BC2
BC2 = 32 + 42 = 9 + 16 = 25
=> BC = 5
Đúng 0
Bình luận (0)
Xem thêm câu trả lời