giúp mik mik cần gấp

chdfxsd

Giả sử a≤b≤c⇒ab+bc+ca≤3bca≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+caabc<ab+bc+ca (1) nên abc<3bc⇒a<3abc<3bc⇒a<3 mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c)2bc<2b+2c+bc⇒bc<2(b+c) (2)

Vì b≤c⇒bc<4c⇒b<4b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5

            Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý

Vì a, b, c có vai trũ như nhau nên giả sử  a   ≤ b   ≤ c  khi đó

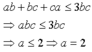
 ( Vì a là số nguyên tố )

Với a = 2 ta có

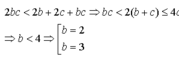
-    Nếu b = 2 thì 4c < 2 + 4c  thoả món với c là nguyên tố bất kỡ

-  Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5

Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .

Em làm cô vui lòng xem giúp em ạ

Có: \(x,y,z>0\)

Nên: \(7^y>1\)

Mà \(7^y+2^z=2^x+1\)(1)

\(\Leftrightarrow2^x>2^z\Rightarrow x>z\)

Xét TH1: y lẻ

Có: \(\left(1\right)\Leftrightarrow2^x-2^z=7^y-1\)

\(\Leftrightarrow2^z\left(2^{x-z}-1\right)=7^y-1\)

Có: y lẻ nên: \(7^y-1=\left(7-1\right)\cdot A=6A⋮6\)

\(\Leftrightarrow7^y-1\equiv2\)(mod 4)

Vì thế: \(2^z=2\)\(\Rightarrow z=1\)(vì với z>1 thì \(2^z\equiv0\)(mod 4)

Thay vào PT: \(2^x-2=7^y-1\)

\(\Leftrightarrow2^x=7^y+1\)

\(\Leftrightarrow2^x=\left(7+1\right)\left(7^{y-1}-7^{y-2}+...-7+1\right)\)

\(\Leftrightarrow2^x=8\left(7^{y-1}-7^{y-2}+...-7+1\right)=8B\)

Vì B lẻ nên: \(2^x=8\)\(\Rightarrow x=3\)\(\Rightarrow y=1\)

Được: \(\left(x;y;z\right)=\left(3;1;1\right)\)

TH2: Khi y chẵn:

\(2^z\left(2^{x-z}-1\right)=7^y-1\)

Vì y chẵn nên: 

\(2^z\left(2^{x-z}-1\right)=\left(7+1\right)\left(7-1\right)C=48C=16\cdot3C\)

Vì: \(2^{x-z}-1\equiv1\)(mod 2)

Nên: \(2^z=16\Rightarrow z=4\)

Thế vào: 

\(2^x+1=7^y+16\)

\(\Leftrightarrow2^x=7^y+15\)

\(\Leftrightarrow2^x=7^y+7+8\)

\(\Leftrightarrow2^x=7\left(7^{y-1}+1\right)+8\)

\(\Leftrightarrow2^x=7\cdot8\cdot\left(7^{y-2}-7^{y-3}+...-7+1\right)+8\)

\(\Leftrightarrow2^x=8\left(7^{y-1}-7^{y-2}+...-7^2+7+1\right)=8S\)

Vì S chia hết cho 8

nên: \(2^x=64P\Rightarrow2^x=64\Rightarrow x=6\)

\(\Rightarrow y=2\)

Vì thế: \(\left(x;y;z\right)=\left(6;2;4\right)\)

Vậy: \(\left(x;y;z\right)=\left(6;2;4\right);\left(3;1;1\right)\)

\(3\)

\(1\)

\(1\)

@ Khôi@ Bài em làm hay lắm.

Tuy  nhiên tại sao \(2^z=16\) em đã biết C có chia hết cho 2 hay ko chia hết cho 2 đâu.

Lí do: Nếu y chẵn thì:

y= 2k ( k nguyên dương  bất kì)

\(2^z\left(2^{x-z}-1\right)=7^y-1=7^{2k}-1=\left(7^k-1\right)\left(7^k+1\right)\)

\(=6.A'.8B'=48.A'.B'=48.C=16.3.C\)

Giả sử như k chẵn chẳng hạn

mình sẽ có: \(A'=7^{k-1}+7^{k-2}+...+7+1\)là số chẵn chia hết cho 2

\(B'=7^{k-1}-7^{k-2}+...+7-1\)là số chẵn chia hết cho 2

khi đó C sẽ chia hết cho 4 là số chẵn 

Thì lúc đấy không thể xảy ra  \(2^z=16\)????? 

cíu zới hiuhiu