Số nghịch đảo của phân số \(\dfrac{a}{b}\)là phân số \(\dfrac{b}{a}\) ; (a ,b ∈ Z , a ≠ 0 , b ≠ 0)

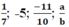Phân số nghịch đảo của phân số  a b là  b a   a ,   b ∈ Z ,   a ≠ 0 ,   b ≠ 0

- Số nghịch đảo của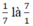 

- Số nghịch đảo của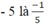 

- Số nghịch đảo của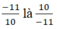 

- Số nghịch đảo của 

a. Gọi phân số cần tìm là \(\frac{a}{b}\)

\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)

Theo bài ra, ta có:

\(\frac{a}{b}+\frac{b}{a}\ge2\)

\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)

\(\Leftrightarrow a^2+b^2\ge2ab\)

\(\Leftrightarrow a^2+b^2-2ab\ge0\)

\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)

\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)

\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)

\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)

\(\Leftrightarrow\left(a-b\right)^2\ge0\)

Vì (a-b)² chắc chắn lớn hơn hoặc bằng 0

\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)

                                Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.

Với a âm thì :

\(\dfrac{1}{a}\) cũng sẽ luôn luôn âm

Với a dương thì:

\(\dfrac{1}{a}\) cũng sẽ luôn luôn dương

Điều này xảy ra vì 1 là số dương,nếu mẫu là âm thì kq âm,và ngược lại