cho tam giác ABC có 3 góc nhọn.Dựng ra phía ngoài 2 tam giác vuông cân đỉnh A là ABD;ACE.Gọi M;N;P lần lượt là trung điểm của BC;BD;CE
a)BE=CD BE vuông góc với CD
b)Tam giác MNP vuông cân
Cho tam giác ABC có 3 góc nhọn. Dựng ra phía ngoài 2 tam giác vuông cân đỉnh A là ABD và ACE . Gọi M;N;P lần lượt là trung điểm của BD; CE; BC .
Chứng minh tam giác MNP vuông cân
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DE
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:
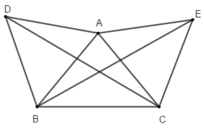
A. 90 o
B. 60 o
C. 45 o
D. 30 o
Xét phép quay tâm A góc quay 60 o biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng DC thành đường thẳng BE suy ra góc giữa DC và BE bằng góc quay 60 o .
Chọn đáp án B.
Cho tam giác ABC có 3 góc nhọn. Dựng ra phía ngoài 2 tam giác vuông can đỉnh A là ABD và ACE. Gọi M;N;P lần lượt là trung điểm của BC;BD;CE.
a) Chứng minh: BE = CD và BE vuoongh góc với CD
b) Chứng minh tam giác MNP vuông cân
a ) Xét góc DAC và góc EAB có
góc ADC = 90 độ + góc ABC (gt) (1)
góc ABE = 90 độ +góc BAC (2)
từ (1) và (2) => góc DAC = góc EAB
Xét tam giác DAC và tam giác EAB có
AD =AB ( vì tam giác ABD vuông cân )
góc DAC = góc BAE
AC =AE
=> tam giác DAC = tam giác EAB ( cạnh - góc - cạnh )
=> DC=EB ( cặp cạnh tương ứng )
+> chứng minh BE vuông góc với CD
Gọi O là giao điểm của DC và BE
Vì góc O1 = O2 ( đối đỉnh )
góc C1 = E1 ( vì tam giác DAC = tam giác EAB ( cmt )
=> góc O = A1 = 90 độ
=> CD vuông góc với BE ( điều phải chứng minh )
a) Xét tam giác DAC và tam giác BAE có:
AB = AD ( tam giác ABD vuông cân tại A )
AC = AE ( tam giác ACE vuông cân tại A )
\(\widehat{DAC}=\widehat{BAE}\)
\(\Rightarrow\Delta DAC=\Delta BAE\left(c-g-c\right)\)
\(\Rightarrow DE=BC\)( hai cạnh tương wungs bằng nhau ) ( 1 )
Ta có: M là trung điểm của BC ; N là trung điểm của BD và P là trung điểm của CE
Suy ra PN là đường trung bình của tam giác BEC \(\Rightarrow PN=\frac{EB}{2}\left(2\right)\)và PN // EB
Suy ra PM là đường trung bình của tam giác BCD \(\Rightarrow PM=\frac{DC}{2}\left(3\right)\)và PM // DC
Từ ( 1 ) ; ( 2 ) và ( 3 ) suy ra PN = PM ( 4 )
\(\widehat{M_1}\)là góc ngoài tại đỉnh M của tam giác EMC nên \(\widehat{M_1}=\widehat{E_1}+\widehat{MCE}=\widehat{E_1}+\widehat{C_1}+\widehat{C_2}\)
Mà \(\widehat{C_2}=\widehat{E_2}\)( Vì tam giác DAC = tam giác BAE cmt )
\(\Rightarrow\widehat{M_1}=\widehat{E_1}+\widehat{C_1}+\widehat{E_2}=\widehat{AEC}+\widehat{C_1}=90^0\)( Tam giác AEC vuông cân tại A )
\(\Rightarrow CD\perp BE\left(đpcm\right)\)
b) Vì \(CD\perp BE\)( Đã chứng minh ở câu a )
Ta có \(BE//PN\Rightarrow PN\perp DC\)
Mà \(PM//DC\Rightarrow PN\perp PM\Rightarrow\widehat{MPN}=90^0\left(5\right)\)
Từ ( 4 ) và ( 5 ) suy ra MNP vuông cân tại P ( đpcm )
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh các tam giác đều ABD và ACE . Góc giữa hai đường thẳng BE và CD là:
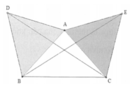
A. 90 °
B. 60 °
C. 45 °
D. 30 °
Đáp án B
Xét phép quay tâm A góc quay 60 ° biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng CD thành đường thẳng BE suy ra góc giữa BE và CD bằng góc quay 60 °
Cho ∆ABC. Về phía ngoài tam giác vẽ các tam giác ABD vuông cân đỉnh B, tam giác ACE vuông cân đỉnh C. Gọi M là giao điểm của BE và CD. CMR: AM vuông góc BC.
Cho tam giác nhọn ABC. Về phía ngoài tam giác ABC vẽ các tam giác ABD vuông cân đỉnh B, tam giác ACE vuông cân đỉnh C. Gọi M là giao điểm của BE và CD. C/m rằng : AM vuông góc BC.
Cho tam giác ABC nhọn.Dựng ở phía ngoài tam giác ABC 2 tam giác vuông ABD và ACE sao cho AD = BD,AE=CE
a.Chứng minh DC = BE
b.DC vuông góc với BE
c.Nếu AC = AB. Chứng minh tam giác ABD = tam giác ACE
d.Gọi M là trung điểm của BC. chứng minh AM vuông góc với DE
Cho tam giác ABC nhọn.Dựng ở phía ngoài tam giác ABC 2 tam giác vuông ABD và ACE sao cho AD = BD,AE=CE
a.Chứng minh DC = BE
b.DC vuông góc với BE
c.Nếu AC = AB. Chứng minh tam giác ABD = tam giác ACE
d.Gọi M là trung điểm của BC
chứng minh AM vuông góc với DE