Cho tam giác ABC vuông tại A các tia phân giác của góc B;C cắt nhau tại I, IH vuông với BC (H thuộc BC ) biết IH =1cm HB =2cm ,HC = 3cm Tính chu vi tam giác ABC

Những câu hỏi liên quan
1. Cho tam giác ABC, góc A 120 độ, AA, BB, CC theo thứ tự là tia phân giác của các góc A, B, C. CMR AB vuông góc với AC.2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD 1/2 MN.3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, AA', BB', CC' theo thứ tự là tia phân giác của các góc A, B, C. CMR A'B' vuông góc với A'C'.
2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD = 1/2 MN.
3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Cho tam giác ABC vuông tại A có góc B=60 °. Tia phân giác của góc ABCcho tam giác abc vuông tại a có góc b = 60 độ . tia phân giác của góc b cắt ac tại e , kẻ eh vuông góc đc tại h a) chứng minh tam giác abe = tam giác hbe b) hb=hc C) từ H kẻ đường thẳng song song với BE cắt AC ở K .c/m🔺AHK là tam giác đều d) gọi I là giao điểm của BA và HE. Chúng minh IE>EH
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A với góc A 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.a.Chứng minh BABIb.Trên tia đối của DB lấy K sao cho DADK. Chứng minh tam giác AIK đềuc.Tính các góc của tam giác BCKCho tam giác ABC cân tại A với góc A 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.a.Chứng minh BABIb.Trên tia đối của DB lấy K sao cho DADK. Chứng minh tam giác AIK đềuc.Tính các góc của ta...
Đọc tiếp
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.Bài 2: Cho tam giác ABC có góc A 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM...
Đọc tiếp
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.
Bài 2: Cho tam giác ABC có góc A= 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.
Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM vuông góc với CN.
Mọi người giúp mình nhanh nha😙😙😙😙
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!
Đúng 0
Bình luận (0)
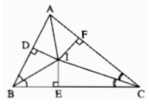
Cho tam giác ABC vuông xuân tại đỉnh A, các tia phân giác trong AD và CE của góc A và góc C cắt nhau tại O. Đường phân giác góc B của tam giác ABC cắt AC tại F a) Góc FBO = 90 độ b)DF là tia phân giác góc D của tam giác ADB c) D , E , F thẳng hàng
Cho tam giác ABC. Các tia phân giác của các góc B và C cát nhau tại I. chứng minh rằng AI là tia phân giác của góc A.
Hướng dẫn: từ I, kẻ các đường vuông góc với các cạnh của tam giác ABC.
Kẻ: ID⊥AB, IE⊥BC, IF⊥AC
Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:
∠(DBI) =∠(EBI) (gt)
∠(IDB) =∠(IEB) =90o
BI cạnh chung
Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)
Suy ra: ID = IE ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:
∠(ECI) =∠(FCI)
∠(IEC) =∠(IFC) =90o
CI cạnh huyền chung
Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:
ID=IF
∠(IDA) =∠(IFA) =90o
AI cạnh huyền chung
Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)
Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)
Vậy AI là tia phân giác góc A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại đỉnh A, các tia phân giác trong AD và CE của góc A và góc C cắt nhau tại O. Đường phân giác góc B của tam giác ABC cắt AC tại F
a) Góc FBO = 90 độ
b) DF là tia phân giác góc D của tam giác ADB
c) D , E , F thẳng hàng
1.Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Chứng minh rằng AI là tia phân giác của góc A.Hướng dẫn: Từ I kẻ các đường thẳng vuông góc với các cạnh của tam giác ABC2.Cho tam giác ABC có AB AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH CK.
Đọc tiếp
1.Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Chứng minh rằng AI là tia phân giác của góc A.
Hướng dẫn: Từ I kẻ các đường thẳng vuông góc với các cạnh của tam giác ABC
2.Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.
1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
Đúng 0
Bình luận (0)
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)
Đúng 0
Bình luận (0)
2. Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.
Xét ∆BMI và ∆CMI, ta có:
+) BM = CM (vì IM là đường trung trực của BC)
+)\(\widehat{BMI}=\widehat{CMI}=90^0\)
+) MI cạnh chung
Suy ra: ∆BMI = ∆CMI (c.g.c)
⇒ IB = IC (hai cạnh tương ứng)
Xét hai tam giác vuông IHA và IKA, có:
+) \(\widehat{HAI}=\widehat{KAI}\) (AI là phân giác góc A)
+) AI cạnh huyền chung
Suy ra: ∆IHA = ∆IKA (cạnh huyền - góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông IHB và IKC, có:
+) IB = IC (chứng minh trên)
+) IH = IK (chứng minh trên)
Suy ra: ∆IHB = ∆IKC (cạnh huyền - cạnh góc vuông)
Suy ra: BH = CK (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
1 ) Cho tam giác ABC có góc B = góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài tại đỉnh A . Chứng minh rằng : Ax//Bc
2 ) Cho tam giác ABC vuông tại A . Vẽ AH vuông góc với BC . Các tia phân giác của các góc BAH và góc C cắt nhau tại K . Chứng minh rằng : AK vuông góc với CK
1.Cho tam giác ABC có A + B = C + 90 và A = C + 10. Tính các góc của tam giác ABC
2.Cho tam giác ABC vuông tại A, vẽ các tia phân giác của B và C cắt nhau tại M. Tính BMC
3.Cho tam giác ABC có A =80, B = 60. Hai tia phân giác của B và c cắt nhau tại I, vẽ tia p/g góc ngoài tại B sao cho B cắt tia CI tại D
a) Tính BIC
b)CMR BDC = C
1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
Đúng 0
Bình luận (0)
2,
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)
Đúng 0
Bình luận (0)



















