LỚP 8:MÌNH CẦN GẤP
GT :hình thang cân ABCD , AB song song CD , BD vuông góc BC , DB là phân giác góc ADC
KL : A ) tính các góc của hình thang ABCD ; B ) cho BC=6cm Tính chu vi hình thang
LỚP 8
GT :hình thang cân ABCD , AB song song CD , BD vuông góc BC , DB là phân giác góc ADC
KL : A ) tính các góc của hình thang ABCD ; B ) cho BC=6cm Tính chu vi hình thang
LỚP 8
GT :hình thang cân ABCD , AB song song CD , BD vuông góc BC , DB là phân giác góc ADC
KL : A ) tính các góc của hình thang ABCD ; B ) cho BC=6cm Tính chu vi hình thang
bài 2 Hình thang cân ABCD (AB//CD) có đường chéo DB vuông góc với cạnh BC. biết đường chéo BD cũng là tia phân giác của góc ADC.
a) tính các góc của hình thang ABCD
giải hộ tôi đâng cần gấp
\(\text{#3107}\)
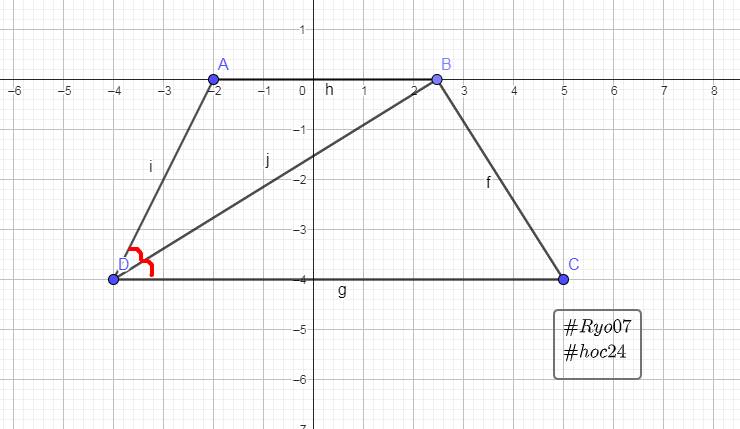
a)
Vì BD là tia phân giác của \(\widehat{\text{ADC}}\)
\(\Rightarrow\widehat{\text{ADB}}=\widehat{\text{CDB}}=\dfrac{1}{2}\widehat{\text{ADC}}\)
Mà ABCD là hình thang cân
\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}\)
\(\Rightarrow\widehat{\text{C}}=2\widehat{\text{BDC}}\)
Xét `\Delta BDC:`
\(\widehat{\text{BDC}}+\widehat{\text{CBD}}+\widehat{\text{C}}=180^0\\ \Rightarrow\widehat{\text{BDC}}+90^0+2\widehat{\text{BDC}}=180^0\\ \Rightarrow3\widehat{\text{BDC}}=90^0\\ \Rightarrow\widehat{\text{BDC}}=30^0\)
Vì \(\widehat{\text{C}}=2\widehat{\text{BDC}}\)
\(\Rightarrow\widehat{\text{C}}=2\cdot30^0\\ \Rightarrow\widehat{\text{C}}=60^0\)
Vì $\widehat{C} = \widehat{D}$
\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}=60^0\)
Vì ABCD là hình thang cân
\(\Rightarrow\widehat{\text{A}}+\widehat{\text{D}}=180^0\left(\text{2 góc trong cùng phía bù nhau}\right)\\ \Rightarrow\widehat{\text{A}}+60^0=180^0\\ \Rightarrow\widehat{\text{A}}=120^0\)
Vì \(\widehat{\text{A}}=\widehat{\text{B}}\left(\text{ABCD là hình thang cân}\right)\)
\(\Rightarrow\widehat{\text{A}}=\widehat{\text{B}}=120^0\)
Vậy, số đo các góc trong hình thang cân ABCD là: \(\widehat{\text{A}}=\widehat{\text{B}}=120^0;\widehat{\text{C}}=\widehat{\text{D}}=60^0.\)
Cho hình thang cân abcd có ab//CD VÀ bd VUÔNG GÓC BC , DB là phân giác ADC
Tính các góc của hình thang ABCD
cần gấp ạ bạn nào làm được mình cho 3 k luôn
Kéo dài DA,cắt BC tại E
Ta có:Xét tam giác DBE và tam giác DBC có:
\(\hept{\begin{cases}\widehat{DBE}=\widehat{DBC}=\left(=90^0\right)\\DBchung\\\widehat{BDE}=\widehat{BDC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta DBE=\Delta DBC\left(g.c.g\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{DCB}\left(1\right)\)
Ta lại có:Vì tứ giác ABCD là hình thang cân có AB song song với CD nên
\(\Rightarrow\widehat{ADC}=\widehat{BCD}\left(2\right)\)
Từ (1) và (2)
Suy ra tam giác DEC là tam giác đều
\(\Rightarrow\widehat{ADC}=\widehat{BCD}=60^0\)
\(\Rightarrow\widehat{DAB}=\widehat{CBA}=\frac{360^0-60^0.2}{2}=120^0\)
Vậy............
cho hình thang cân ABCD(ABsong song với DC)có DB là tia phân giác của góc ADC,BD vuông góc BC,AB=4cm.Tính chu vi hình thang cân
Cho hình thang cân ABCD (AB//CD) có DB vuông góc với BC và DB là tia phân giác của góc ADC. a, Tính các góc của hình thang b, Biết BC = 6cm. Tính chu vi hình thang (giúp mình với ạ)
a) Gọi \(\widehat{ADB}=\widehat{D_1;}\widehat{CDB}=\widehat{D_2}\)
Xét Δ vuông BDC ta có :
\(\)\(\widehat{D_2}+\widehat{C}=90^o\)
mà \(\widehat{D_2}=\dfrac{\widehat{D}}{2}\) (DB là phân giác \(\widehat{ADC}\))
\(\widehat{C}=\widehat{D}\) (ABCD là hình thang cân)
\(\Rightarrow\dfrac{\widehat{D}}{2}+\widehat{D}=90^o\)
\(\Rightarrow\dfrac{\widehat{3D}}{2}=90^o\Rightarrow\widehat{D}=60^o\Rightarrow\widehat{C}=\widehat{D}=60^o\)
Ta lại có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
mà \(\left\{{}\begin{matrix}\widehat{A}=\widehat{B}\\\widehat{C}=\widehat{D}\end{matrix}\right.\) (ABCD là hình thang cân)
\(\Rightarrow2\widehat{A}+2\widehat{C}=360^o\Rightarrow\widehat{A}=\widehat{B}=\dfrac{360^o-2\widehat{C}}{2}\)
\(\Rightarrow\widehat{A}=\widehat{B}=\dfrac{360^o-2.60^o}{2}=120^o\)
b) \(BC=AD=6\left(cm\right)\) (ABCD là hình thang cân)
Xét Δ vuông BDC ta có :
\(Cos60^o=\dfrac{BC}{DC}=\dfrac{1}{2}\)
\(\Rightarrow DC=2BC=2.6=12\left(cm\right)\)
\(DC^2=BD^2+BC^2\left(Pitago\right)\)
\(\Rightarrow BD^2=DC^2-BC^2=12^2-6^2=144-36=108=3.36\)
\(\Rightarrow BD=6\sqrt[]{3}\left(cm\right)\)
Kẻ đường cao AH và BE vuông góc DC tại H và E
Ta có : \(BE.CD=BD.BC\Rightarrow BE=\dfrac{CD}{BD.BC}=\dfrac{12}{6.6\sqrt[]{3}}=\dfrac{1}{3\sqrt[]{3}}\left(cm\right)\)
Xét Δ BEC ta có :
\(BC^2=BE^2+EC^2\Rightarrow EC^2=BC^2-BE^2=36-\dfrac{1}{27}\)
\(\Rightarrow EC^2=\dfrac{971}{27}\Rightarrow EC=\dfrac{1}{3}.\sqrt[]{\dfrac{971}{3}}\left(cm\right)\)
ABHE là hình chữ nhật (AB \(//\) HE;AH \(//\) BE vì cùng vuông với CD; Góc H=90o )
\(\Rightarrow AB=HE=CD-2EC=12-\dfrac{2}{3}.\sqrt[]{\dfrac{971}{3}}\left(cm\right)\) (tính chất hình thang cân)
Chu vi hình thang cân ABCD :
\(2BC+DC+AB=2.6+12+12-\dfrac{1}{3}.\sqrt[]{\dfrac{971}{3}}=36-\dfrac{1}{3}.\sqrt[]{\dfrac{971}{3}}\left(cm\right)\)
a/
\(\widehat{ADB}=\widehat{CDB}=\dfrac{\widehat{ADC}}{2}\) (gt)
Mà \(\widehat{ADC}=\widehat{BCD}\) (góc ở đáy hình thang cân)
\(\Rightarrow\widehat{CDB}=\dfrac{\widehat{BCD}}{2}\)
Xét tg vuông BCD có
\(\widehat{CDB}+\widehat{BCD}=90^o\Rightarrow\dfrac{\widehat{BCD}}{2}+\widehat{BCD}=90^o\Rightarrow\widehat{BCD}=60^o\)
\(\Rightarrow\widehat{CDB}=\dfrac{\widehat{BCD}}{2}=\dfrac{60^o}{2}=30^o\)
\(\Rightarrow\widehat{ADC}=\widehat{BCD}=60^o\)
Ta có
\(\widehat{DAB}=\widehat{ABC}\) (góc ở đáy hình thang cân)
\(\widehat{DAB}=180^o-\widehat{ADC}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{DAB}=\widehat{ABC}=120^o\)
b/ Từ B dựng đường thẳng // AD cắt CD tại E ta có
AB // CD => AD//DE mà BE//AD
=> ABED là hình bình hành
=> BE = AD mà AD = BC (cạnh bên hình thang cân)
=> BE = AD = BC = 6 cm
Xét tg BCE có
BE = BC => tg BCE cân tại B
\(\Rightarrow\widehat{BEC}=\widehat{BCD}=60^o\Rightarrow\widehat{CBE}=60^o\) => tg BCE là tg giác đều
=> BE = CE = BC = 6 cm
Xét tg vuông BCD có
\(\widehat{CDB}=30^o\) (cmt) => \(BC=\dfrac{CD}{2}\) (trong tg vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)
\(\Rightarrow CD=2BC=2.6=12cm\)
\(\Rightarrow DE=CD-CE=12-6=6cm\)
Mà DE = AB = 6 cm (cạnh đối hbh ABED)
\(\Rightarrow C_{ABCD}=AB+BC+CD+AD=6+6+12+6=30cm\)
Ta có DB là tia pgiac của \(\widehat{ADC}\)
Mà \(\widehat{ADC}=\widehat{BCD}\) do 2 góc là góc đáy của hình thang
=>\(\widehat{BDC}=\widehat{DCB}:2\)
Xét ∆ vuông BDC có:
\(\widehat{BDC}+\widehat{DCB}=90^o=>\widehat{DCB}:2+\widehat{DCB}=90^o\)
\(\Rightarrow\widehat{DCB}=60^o\\ \Rightarrow\widehat{BDC}=60^o:2=30^O\)
Ta có: \(\widehat{BAD}=\widehat{ABC}\) (t/chất hthang)
\(\Rightarrow\widehat{BAD}=180^o-\widehat{BDC}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{BAD}=\widehat{ABC}=120^o\)
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của A D C ^ .
a) Tính các góc của hình thang cân ABCD.
b) Biết BC = 6 cm, tính chu vi và diện tích của hình thang cân ABCD
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
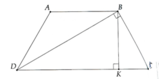
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của góc ADC
a) Tính các góc của hình thang cân ABCD
b) Biết BC=42cm. Tính chu vi và diện tích của hình thang ABCD
Nhận cày thuê điểm hỏi đáp nha...
Quan tâm ib mình!!