Cho tam giác ABC vuông tại A,vẽ đường cao AH.ChoAB=6cm;AC=8cm
a/ Chứng minh ΔHBA đồng dạng ΔABC
b/ Tính BC,AH,BH

Những câu hỏi liên quan
Cho tam giác ABC có AB 6cm, AC 8cm, BC 10cm. Vẽ đường cao AD của tam giác ABC. a) Chứng minh tam giác ABC vuông tại A và tam giác ABD đồng dạng tam giác CAD. b) Trên AB lấy điểm F sao cho AB 3AF. Từ điểm D, vẽ đường thẳng vuông góc với FD tại D, đường thẳng này cắt AC tại E. Chứng minh: góc AFD góc CED. c) Tính tỉ số: CECA����
Đọc tiếp
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Vẽ đường cao AD của tam giác ABC. a) Chứng minh tam giác ABC vuông tại A và tam giác ABD đồng dạng tam giác CAD. b) Trên AB lấy điểm F sao cho AB = 3AF. Từ điểm D, vẽ đường thẳng vuông góc với FD tại D, đường thẳng này cắt AC tại E. Chứng minh: góc AFD = góc CED. c) Tính tỉ số:
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét ΔABD vuông tại D và ΔCAD vuông tại D có
góc DBA=góc DAC
=>ΔABD đồng dạng với ΔCAD
b: góc EAF+góc EDF=180 độ
=>AFDE nội tiếp
=>góc AFD+góc AED=180 độ
=>góc AFD=góc CED
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,
B
^
35
0
và AB 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABCGiải tam giác ABC. A. AC 8,57cm; BC 10,46cm;
C
^
55
0
. B. AC 4,9cm; BC 7,75cm;
C
^
55
0
. C....
Đọc tiếp
Cho tam giác ABC vuông tại A, B ^ = 35 0 và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC
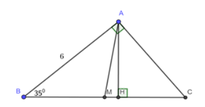
Giải tam giác ABC.
A. AC = 8,57cm; BC = 10,46cm; C ^ = 55 0 .
B. AC = 4,9cm; BC = 7,75cm; C ^ = 55 0 .
C. AC = 4,2cm; BC = 7,32cm; C ^ = 55 0 .
D. AC = 3,44cm; BC = 6,92cm; C ^ = 55 0 .
Xét ∆ ABC vuông tại A ta có:
Vì ∆ ABC vuông tại A ta có:
![]()
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC vuông tại A có góc B= 30o, AB=6cm
a. Tính tam giác vuông ABC
b. Vẽ đường cao AH và trung tuyến AM của tam giác ABC. Tính diện tích tam giác AHM
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=2\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm a) Tính BC b) Vẽ đường cao AH. Chứng minh tam giác ABC đồng dạng tam giác HBA c) Tính HB,HC
a: BC=căn 6^2+8^2=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
c: HB=AB^2/BC=6^2/10=3,6cm
HC=10-3,6=6,4cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A biết AB = 6cm, BC = 10cm
a.Tính diện tích tam giác ABC.
b. Tính đường cao AH.
Khỏi vẽ hình cx đc:))
a. Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2 (định lý Py-ta-go)
=>62+AC2=BC2
=>AC=8 cm.
=> SABC=AB.AC=6.8=48 (cm)
b. Ta có: SABC=AB.AC=BC.AH
=>6.8=10.AH
=>AH=4,8 cm.
Đúng 2
Bình luận (0)
a/
diện tích tam giác ABC là:
\(\dfrac{6.10}{2}\)=30 (cm2)
đường cao AH là
30:10=3 cm
Đúng 0
Bình luận (0)
a. Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2 (định lý Py-ta-go)
=>62+AC2=BC2
=>AC=8 cm.
=> SABC=AB.AC=\(\dfrac{6.8}{2}\)=24 (cm2)
b. Ta có: SABC=AB.AC=BC.AH
=>6.8=10.AH
=>AH=4,8 cm.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A vẽ đường cao AH,AB= 6cm,AC= 8cm
A,Chứng minh tam giác HBA đồng dạng tam giác ABC
B, tính BC,AH,BH
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a vẽ đường cao ah, ab =6cm,ac=8cm a,Chứng minh tam giácHBA đồng dạng với tam giác abc b,chứng minh ah2=hb nhân hc
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. AB 6cm, AC 8cm. Vẽ đường cao AH.
a) CMR: tam giác ABC đồng dạng tam giác HAC. AB×AC=BC×AH
b) Tính BC, BH
c) Vẽ HD vuông góc với AB tại D, HE vuông góc với AC tại E. Chứng minh AB×AD+AC×AE=2DE^2
Xem chi tiết
cho tam giác ABC vuông tại A vẽ đường cao AH,AB=6cm,AC=8cm
a) chứng minh tam giác HBA đồng dạng với tam giác ABC
b)Tính BC,AH,BH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB^2=6^2-4,8^2=3,6^2\)
=>HB=3,6(cm)
Đúng 0
Bình luận (0)


















