cho hình vẽ biết \(aa'//bb';A4=60\)
a \(c\perp aa'\)
b tính bBA
c gọi à và By lần lượt là tia p/g DAB,bBA
c/m Ax//by
Cho hình vẽ. Biết a'Mc = 100⁰ và b'Nc' = 80⁰. Chứng minh aa' // bb'
Ta có: \(\widehat{a'Mc}+\widehat{a'MN}=180^o\)(Hai góc kề bù)
\(\Rightarrow\widehat{a'MN}=180^o-\widehat{a'Mc}=180^o-100^o=80^o\)
Do \(\widehat{a'MN=\widehat{b'Nc'}\left(=80^o\right)}\)
Mà hai góc này ở vị trí đồng vị
\(\Rightarrow aa'\)//\(bb'\)
#YM
Cho hình vẽ bên, biết c A a ' ^ = 120 ° và A B b ^ = 60 ° . Hai đường thẳng aa' và bb' có song song với nhau không? Vì sao?
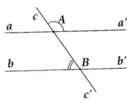
Cho hình vẽ bên, biết c A a ' ^ = 120° và A B b ^ = 60°. Hai đường thẳng aa' và bb' có song song với nhau không? Vì sao?
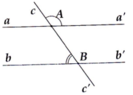
Ta có: c A a ' ^ + a ' A B ^ = 180° (hai góc kề bù)
=> a ' A B ^ = 180 ° − c A a ' ^ = 180 ° − 120 ° = 60 °
=> a ' A B ^ = A B b ^ = 60 ° (hai góc so le trong bằng nhau)
=> aa' // bb'
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
giúp mình với
Cho hình đa diện như hình vẽ, trong đó các cạnh AA’, BB’, CC’ đều vuông góc với (ABC), tam giác ABC đều cạnh a và A A ' = B B ' = 1 2 C C ' = a . Tính theo a thể tích V của khối đa diện đó.
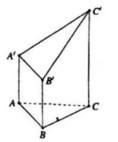
A. V = a 3 3 6 .
B. V = a 3 3 3 .
C. V = 4 a 3 3 3 .
D. V = 3 a 3 3 4 .
Phương pháp:
Cắt khối đa diện đã cho làm hai khối: khối lăng trụ và khối tứ diện.
Cách giải:
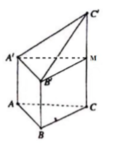
Gọi M là trung điểm của CC’.
Khi đó: khối đa diện đã cho được chia làm 2 phần: Khối lăng trụ tam giác đều A’B’M.ABC và khối tứ diện A’B’C’M.
Thể tích khối lăng trụ tam giác đều A’B’M.ABC là:
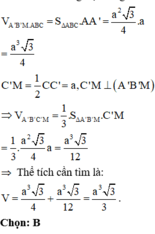
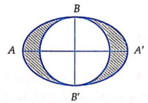
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA’=8 và độ dài trục nhỏ là BB’=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA'=8 và độ dài trục nhỏ là BB'=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
Đáp án B
Thể tích của khối tròn xoay thu được khi quay elip có trục lớn A A ' = 8 , trục nhỏ B B ' = 6 khi quay quanh trục AA’ là V E = 4 3 π . A A ' 2 . B B ' 2 2 = 4 3 π .4.3 2 = 48 π (đvtt).
Thể tích khối tròn xoay thu được khi quay đường tròn O ; B B ' 2 quanh trục AA’ cũng chính là thể tích khối cầu tâm O, bán kính R = 3 . Thể tích đó là
V O ; 3 = 4 3 π R 3 = 4 3 π .3 3 = 36 π (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = V E − V O ; 3 = 48 π − 36 π = 12 π (đvtt)
Vẽ hai đường thẳng aa' và bb' vuông góc với nhau tại M, trên đường thẳng aa' lấy hai điểm A, B sao cho M là trung điểm của AB. Trên đường thẳng bb' lấy hai điểm C, D sao cho CM=MD. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb' là đường trung trực của đoạn thẳng AB và đường thẳng aa' là đường trung trực của đoạn thẳng CD.
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
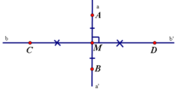
: Vẽ hai đường thẳng aa’ và bb’ vuông góc với nhau tai M, trên đường thẳng aa’ lấy hai điểm AB sao cho M là trung điểm của AB. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb’ là đường trung trực của đoạn thẳng AB