cho hình vẽ trong đó Ax//Dy;A,C,D thẳng hàng
a, chứng minh góc xAC+ACB+CBy=360 độ
b,tính số đo của tam giác BCD nếu biết góc xAD=11độ và góc yBC-ACB=30 độ
Những câu hỏi liên quan
Cho hình vẽ, biết Ax//Dy, góc xAd= 100 độ
a) Tính góc ADy
b) Biết góc ADE=110 độ, góc DEz=30 độ. Chứng minh Dy//Ez
c) Ax có song song với Ez không? vì sao
Cho Ax // Dy,số đo các góc trên hình vẽ,tính BCD biết góc B 120 độ,góc D 30 độ
Xem chi tiết
bài 2: cho hình vẽ biết:: Ax//Dy. chứng minh rằng A^+B^+O^=360 độ
Cho hình vẽ, biết Ax // Dy. Chứng minh: OB vuông góc với OC
Kéo dài BO cắt Dy tại N
\(\Rightarrow\widehat{ABN}=\widehat{BNC}=60^o\) (góc so le trong)
Xét tg ONC có
\(\widehat{NOC}=180^o-\left(\widehat{BNC}+\widehat{OCN}\right)=180^o-\left(60^o+30^o\right)=90^o\Rightarrow OB\perp OC\)
Cho tam giác ABC và DBC vuông có chung cạnh huyền BC(A và D cùng 1 nửa mp bờ BC). vẽ tia Ax sao cho AC là pg góc DAx. vẽ tia Dy sao cho DB là pg ADy. Ax cắt Dy tại E. Gọi O là giao điểm của AC và BD. CMR: OE vuông góc với BE
Bài 5: Cho hình thang ABCD (AB//CD), biết Ax,Dy lần lượt là phân giác của góc A, góc D của hình thang. Chứng minh Ax vuông góc với Dy
Bài 6: Cho hình thang ABCD (AB//CD,AB<CD). Qua B kẻ đường thẳng song song với AD cắt CD tại E. Chứng minh:
a) AD=BE , AB=DE
b) CD-AB=CE
c) BC+AD>CD_AB
Bài 5
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
Đúng 1
Bình luận (0)
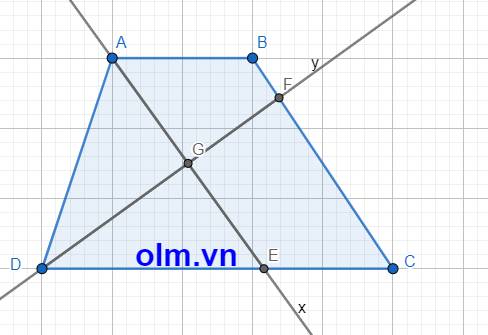
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)
Đúng 0
Bình luận (0)
Cho 2 tam giác ABC và DBC chung cạnh huyền BC (A,D thuộc cùng một nửa mặt phẳng BC). Vẽ tia Ax sao cho AC là phân giác góc DAx. Vẽ tia Dy sao cho DB là phân giác góc ADy; Ax cắt Dy tại E, O là giao điểm Ac và BD
a) Chứng minh OE vuông góc BE
b) Chứng minh B,E,C thẳng hàng
cho tam giác abc và dbc chung cạnh huyền bc. a và d nằm trên nửa mặt phẳng bờ bc vẽ tia ax sao cho ac là p/g của dax. vẽ tia dy sao cho bd là p/g của ady. ax cắt dy tại e
a) c/m oeb thẳng hàng
b)c/m ba điểm ceb thẳng hàng
Cho hình bên.Biết AD ⊥ DC,
∠
DAC
74
°
,
∠
AXB
123
°
, AD 2,8cm, AX 5,5cm, BX 4,1cm.Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY
Đọc tiếp
Cho hình bên.
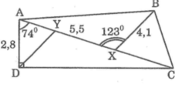
Biết AD ⊥ DC, ∠ DAC = 74 ° , ∠ AXB = 123 ° , AD = 2,8cm, AX = 5,5cm, BX = 4,1cm.
Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY
