Các câu hỏi tương tự
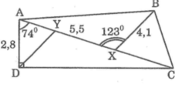
Cho hình bên.Biết AD ⊥ DC,
∠
DAC
74
°
,
∠
AXB
123
°
, AD 2,8cm, AX 5,5cm, BX 4,1cm.Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY
Đọc tiếp
Cho hình bên.
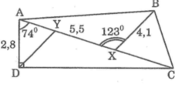
Biết AD ⊥ DC, ∠ DAC = 74 ° , ∠ AXB = 123 ° , AD = 2,8cm, AX = 5,5cm, BX = 4,1cm.
Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY
AD vuông góc với DC, ^DAC = 74 ^AXB = 123, AD = 2,8cm, AX = 5,5cm, BX = 4,1cm
a) Tính AC
b) Gọi Y là điểm trên AX sao cho DY//BX. Hãy tính XY
c) Tính diện tích tam giác BCX
Cho hình bên.Biết AD ⊥ DC,
∠
DAC
74
°
,
∠
AXB
123
°
, AD 2,8cm, AX 5,5cm, BX 4,1cm.Tính AC
Đọc tiếp
Cho hình bên.
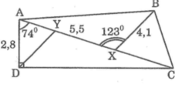
Biết AD ⊥ DC, ∠ DAC = 74 ° , ∠ AXB = 123 ° , AD = 2,8cm, AX = 5,5cm, BX = 4,1cm.
Tính AC
cho nửa đường tròn tâm o , đường kính ab. kẻ 2 tiếp tuyến ax ,bx (ax,bx và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ ab).gọi c là một điểm trên tia ax, kẻ tiếp tuyến cm vs nửa đường tròn (m là tiếp điểm),cm cắt by ở da. tính số đo góc codb.gọi i là giao điểm của oc và am , k là giao điểm của od và mb.tứ giác oimk là hình j? vì saoc.c/m tích ac , bd không đổi khi c di chuyển trên axd. c/m ab là tiếp tuyến của đường tròn đương kính cp()
Đọc tiếp
cho nửa đường tròn tâm o , đường kính ab. kẻ 2 tiếp tuyến ax ,bx (ax,bx và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ ab).gọi c là một điểm trên tia ax, kẻ tiếp tuyến cm vs nửa đường tròn (m là tiếp điểm),cm cắt by ở d
a. tính số đo góc cod
b.gọi i là giao điểm của oc và am , k là giao điểm của od và mb.tứ giác oimk là hình j? vì sao
c.c/m tích ac , bd không đổi khi c di chuyển trên ax
d. c/m ab là tiếp tuyến của đường tròn đương kính cp()
Cho tam giác cân abc gọi d là 1 điểm trên cạnh bc trên nửa mặt phẳng bờ bc không chứa điểm A kẻ tia Bx sao cho CBx = CAD , tia Bx cắt AD ở E . CMR tích AD x AE không đổi khi D thay đổi trên BC
cho ( O;R ) đuờng kính AB từ điểm B kẻ tia tiếp tuyến Bx với (O). trên Bx lấy điểm C, AC cắt (O) tại D từ O kẻ OH vuông góc AD (H thuộc AD ) 1) CMR: HA=HD 2) CMR: BD vuông góc AD và tích AC.AD khong đổi khi C di chuyển trên tia Bx 3)gọi M là trung điểm của BC CMR MD là tiếp tuyến của (O) 4) gọi K là giao điểm của OM và BD xác định vị trí C trên tia BX để tứ giác OHDK là hình vuông
Cho nửa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx với nửa đường tròn, gọi C là điểm trên nửa đường tròn sao cho cung CA bằng cung CB, D là điểm tuỳ ý trên trục khung CB , các tia AC, AD cắt tia BX theo thứ tự tại E và F a, Tính số đo góc AEB b, Chứng minh tứ giác CDFE nội tiếp đường tròn
Câu 1: a) Cho hàm số y ax + b, xác định a,b biết đồ thị hàm số đi qua điểm A( -1;2) và song song với đường thẳng y 2x+3, vẽ đồ thị hàm số với giá trị a, b vừa tìm được b) Cho hàm số : y mx – m + 2, có đồ thị là đường thẳng (d) Tìm tọa độ điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của m c) Tìm m để đường thẳng d cắt đường thẳng y 2x -3 tại điểm nằm trên trục hoành. Câu 2: Cho đường tròn tâm O đường kính AB. Trên đường tròn lấy điểm C sao cho AC BC (C khác A). Tiếp...
Đọc tiếp
Câu 1: a) Cho hàm số y = ax + b, xác định a,b biết đồ thị hàm số đi qua điểm A( -1;2) và song song với đường thẳng y = 2x+3, vẽ đồ thị hàm số với giá trị a, b vừa tìm được b) Cho hàm số : y = mx – m + 2, có đồ thị là đường thẳng (d) Tìm tọa độ điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của m c) Tìm m để đường thẳng d cắt đường thẳng y = 2x -3 tại điểm nằm trên trục hoành. Câu 2: Cho đường tròn tâm O đường kính AB. Trên đường tròn lấy điểm C sao cho AC < BC (C khác A). Tiếp tuyến Bx của đường tròn (O) cắt đường trung trực của BC tại D. Gọi F là giao điểm của DO và BC. a) Chứng minh CD là tiếp tuyến của đường tròn (O) b) Gọi E là giao điểm của AD với đường tròn (O) (với E khác A). Chứng minh DE.DA = DC^2 = DF.DO c) Gọi H là hình chiếu của C trên AB, I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH.
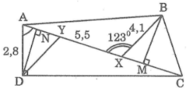
Cho tam giác ABC vuông tại A. Dựng điểm D trên cạnh AC sao cho widehat{DBC}frac{1}{3}widehat{ABC}. Gọi X là hình chiếu vuông góc của C trên đường thẳng BD. Trên tia BA lấy điểm Y sao cho BX BY. Chứng minh rằng a) frac{1}{BY^2}+frac{1}{CX^2}frac{4}{XY^2}b) widehat{XAC}widehat{DBC}từ đó suy ra AX XYc) coswidehat{ABC}4cos^2frac{widehat{ABC}}{3}-3cosfrac{widehat{ABC}}{3}
Đọc tiếp
Cho tam giác ABC vuông tại A. Dựng điểm D trên cạnh AC sao cho \(\widehat{DBC}=\frac{1}{3}\widehat{ABC}\). Gọi X là hình chiếu vuông góc của C trên đường thẳng BD. Trên tia BA lấy điểm Y sao cho BX = BY. Chứng minh rằng
a) \(\frac{1}{BY^2}+\frac{1}{CX^2}=\frac{4}{XY^2}\)
b) \(\widehat{XAC}=\widehat{DBC}\)từ đó suy ra AX = XY
c) \(cos\widehat{ABC}=4cos^2\frac{\widehat{ABC}}{3}-3cos\frac{\widehat{ABC}}{3}\)