Một cạnh của tam giác có trung điểm là M(-1;1), hai cạnh kia nằm trên hai đường thẳng: d1: 2x + 6y +3 = 0 và d2: x + y - 2 = 0. Viết phương trình cạnh thứ 3

Những câu hỏi liên quan
Cho một tam giác đều ABC cạnh a. Tam giác {A_1}{B_1}{C_1} có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác {A_2}{B_2}{C_2} có các đỉnh là trung điểm các cạnh của tam giác {A_1}{B_1}{C_1}, ldots , tam giác {A_{n + 1}}{B_{n + 1}}{C_{n + 1}} có các đỉnh là trung điểm các cạnh của tam giác {A_n}{B_n}{C_n}, ldots Gọi {p_1},{p_2}, ldots ,{p_n}, ldots và {S_1},{S_2}, ldots ,{S_n}, ldots theo thứ tự là chu vi và diện tích của các tam giác {A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, ldots ,{A_n}{B_n...
Đọc tiếp
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Tham khảo:
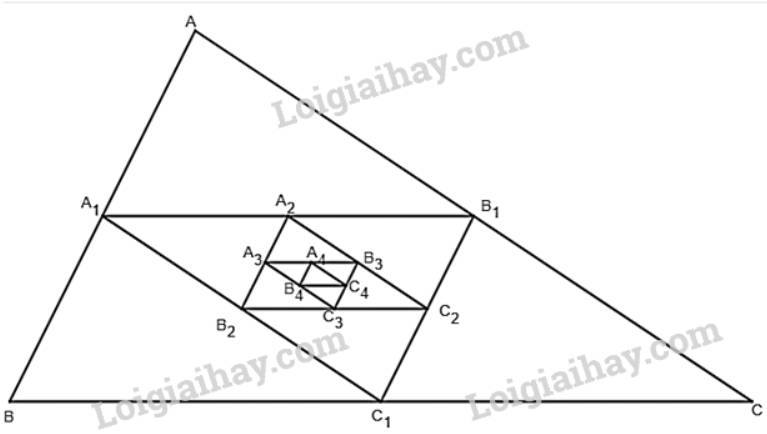
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC.Lấy M là cạnh trung điểm của cạnh AB ;N là cạnh trung điểm của cạnh BC.Nối M với N ta được 1 tứ giác BMNC có diện tích bang 225 cm2 .Tính diện tích tam giác ABC
Một hình tam giác ABC có M là trung điểm của cạnh AB; N là trung điểm của cạnh AC. Kẻ đoạn thẳng BN
A) So sánh diện tích của tam giác AMN và tam giác ABN
B) So sánh diện tích tam giác AMN và tam giác ABC
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 ,..., S n ,... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội
q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 , ... , S n , ... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
Cho hình tam giác ABC.Trên AB lấy điểm M,M là trung điểm của cạnh AB.Trên cạnh AC lấy điểm N,N là trung điểm của cạnh AC.Nối M với N ta được hình tứ giác MNBC có diện tích là 256cm2.Tính diện tích tam giác ABC.
Cho tam giác ABC có diện tích là 48,8 cm2. M là trung điểm của cạnh AB. N là trung điểm của cạnh AC. Tính diện tích tam giác AMN
Sabn=1/2Sabc=48,8:2=24,4m2
Samn=1/2Sabn=24,4:2=12,2m2
Đúng 0
Bình luận (0)
1)Cho tam giác ABC(ABAC)có đường cao AH.Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CA,AB.a)C/m NP là đường trung trực của đoạn AHb)C/m tứ giác MNPH là hình thang cân.2)Cho tam giác ABC có chu vi 20cm.Gọi O là một điểm nằm trong tam giác;D,E,F lần lượt là trung điểm của OA;OB;OC.Tính chu vi tam giác DEF.3)Cho tam giác ABC có AM là trung tuyến.Gọi I là trung điểm của AM,gọi D là giao điểm của BI à AC.a)C/m AD1/2.DCb)So sánh độ dài BD và ID.
Đọc tiếp
1)Cho tam giác ABC(AB<AC)có đường cao AH.Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CA,AB.
a)C/m NP là đường trung trực của đoạn AH
b)C/m tứ giác MNPH là hình thang cân.
2)Cho tam giác ABC có chu vi 20cm.Gọi O là một điểm nằm trong tam giác;D,E,F lần lượt là trung điểm của OA;OB;OC.Tính chu vi tam giác DEF.
3)Cho tam giác ABC có AM là trung tuyến.Gọi I là trung điểm của AM,gọi D là giao điểm của BI à AC.
a)C/m AD=1/2.DC
b)So sánh độ dài BD và ID.
bài 1: Cho tam giác ABC có diện tích là 160cm2 và M là trung điểm chính giữa của cạnh AB
a) Tính diện tích tam giác ACM
b) Tìm trên cạnh AC một điểm N sao cho diện tích tam giác AMN bằng 20cm2.
bài 2: Cho tam giác ABC. trên cạnh BC lấy điểm M sao cho BM= 2MC, trên cạnh AC lấy điểm N sao cho CN=3NA. Tính diện tích tam giác CMN là 20cm2
Cho tam giác ABC có diện tích là 480cm2 .M là trung điểm của cạnh AC ;N là trung điểm của cạnh AB; I là trung điểm của cạnh BC.Tính diện tích tam giác MNI.
CÁC BẠN GIẢI NHANH GIÚP MÌNH !!!! ^_^
Bài này vẽ hình và thêm nhiều đoạn.
Ta đi tìm 3 tam giác bên ngoài: ANM, MIC và NBI rồi lấy tổng 480 trừ 3 hình này sẽ ra hình ở giữa.
Chỉ cần tìm 1 hình và các hình khác tìm tương tự.
S(ABM)=1/2 S(ABC) vì chung chiều cao kẻ từ B và đáy AM=1/2AC
Cũng chung chiều cao và đáy nọ gấp đôi đáy kia ta có: S(ANM)=1/2S(ABM)
Suy ra S(ANM)=1/4 S(ABC)=480:4=120 cm2
Giống như vậy cho 2 tam giác còn lại.
--> S(MNI)= 480-120-120-120=120 cm2
Bạn tự trình bày nhé
Đúng 0
Bình luận (0)


















