Cho hình chữ nhật ABCD có tâm \(I\left(\frac{1}{2};0\right)\) đường thẳng chứa cạnh AB có phương trình : \(x-2y+2=0\) và \(AB=2AD\).
Tìm tọa độ các đỉnh của hình chữ nhật, biết rằng đỉnh A có hoành độ âm.
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0; 3); D(2; 1) và I(-1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC
A. (1 ; 2)
B. (-2; -3)
C. (-3 ; -2)
D. (- 4 ; -1)
Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2)
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra
x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0 ; 3) ; D(2 ; 1) và I( -1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC.
A. (1; 2)
B. (-2; -3)
C. (-3; -2)
D. (-4; -1)
Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2).
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC.
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Cho hình thang ABCD
a. Chỉ ra 1 hình chữ nhật (H) đồng phân với hình thang ABCD (có chứng minh)
b. Với hình chữ nhật(H) đã tìm được ở câu a và cho biết diện tích hình thang ABCD được tính như sau:
\(\frac{\left(a+c\right).b}{2}\). Hãy tìm diện tích hình chữ nhật(H)
cho hình chữ nhật ABCD có AD=1/2 AB=a, I là trọng tâm của tam giác ABD
CM: vecto IA + vecto IB + vecto IC = vecto DC
cho hình bên gồm hình chữ nhật abcd có ad=2dm và 1 nửích phần đã a hình tròn tâm o bán kính 2 dm. tính diện tích phần đã tô đậm cua hình chữ nhật abcd
Cho hình chữ nhật ABCD có tâm I và cạnh AB = 1, AD = √3. Tính số đo các góc ∠(AID) và ∠(DIC) .
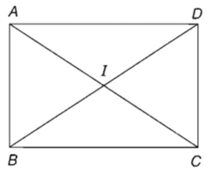
Xét ΔABD vuông tại A có:
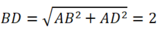
Do ABCD là hình chữ nhật tâm I nên:
AI = IC = ID = 1/2 BD = 1
ΔICD có ID = IC = DC = 1
⇒ΔICD đều ⇒ ∠(DIC) = 60o
Ta có: ∠(DIC) + ∠(AID ) = 180o⇒ ∠(AID ) = 180o- 60o= 120o
Bài 1: Cho hình chữ nhật ABCD có tâm O.Hỏi có bao nhiêu phép quay tâm O, góc quay \(\alpha\), \(0\leq\alpha\leq2\pi\), biến hình chữ nhật thành chính nó?
Bài 2: Cho tam giác đều ABC có tâm O. Phép quay tâm O, góc quay \(\varphi\) biến tam giác đều thành chính nó thì quay \(\varphi\) là góc nào?
Bài 3 Chọn 12 giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu độ?
Bài 4: Cho lục giác đều ABCDEF, O là tâm đối xứng của nó, I là trung điểm AB. Tìm ảnh của tam giác AOF qua phép quay tâm E góc quay \(60^0\)
Bài 5: Trong mặt phẳng Oxy, cho I(2;1) và đường thẳng d: 2x+3y+4=0. Tìm ảnh của d qua \(Q_{(I;45^0)}\)
Bài 6: Trong mặt phẳng Oxy, cho phép tâm O góc quay \(45^0\). Tìm ảnh của đường tròn \((C): (x-1)^2+y^2=4\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc A C B ^ = 30 ∘ . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. a 3 6
D. 4 a 3 3