Đúng/sai Đường tròn (C') tâm I(1;0) tiếp xúc với đường tròn (C) có phương trình (x-1)² + y² =2

Những câu hỏi liên quan
Cho hình tròn tâm a bán kính 2 cm hình tròn tâm b bán kính 4 cm .ghi đúng hoặc sai vào các đâp an.A:Đường kính của hình tròn tâm a có độ dài là 4 cm B: đường kính hình tròn tâm b có bán kính là 2cm C: đường kính của hình tròn tâm a dai mgaaps đôi đường kính hình tròn tâm b.D: đường kính của hình tròn tâm b dài gấp 4 lần đường kính của hình tròn tâm a
Bán kính hình tròn đó là:
6:2=3( cm )
Đáp số:3 cm
Đúng 0
Bình luận (0)
đúng ghi Đ , sai ghi S :
a, điểm a ở trong hình tròn tâm O.
b, điểm a ở trên đường tròn tâm O.
c, điểm b ở trên đường tròn tâm O .
d, điểm c ở ngoài hình tròn tâm O.
ai nhanh mình tik.
Xin hình đi bạn ơi ! Không có hình thì làm kiểu j ?
Câu nào đúng, câu nào sai hay cả hai cùng đúng hoặc cùng sai?
- Bán kính là một đoạn thẳng đi qua tâm của hình tròn và bằng một nửa đường kính.
- Bán kính là một đoạn thẳng nối một điểm trên đường tròn với tâm của hình tròn.
Xem thêm câu trả lời
Đúng hay sai :
Nếu điểm M nằm bên trong đường tròn tâm O thì M cách điểm O một khoảng nhỏ hơn bán kính đường tròn tâm O.
Đ nha
------H-------------------T-------------
trung điểm của đường kính là tâm của hình tròn đúng hay sai?
Xét tính đúng – sai của mỗi khẳng định sau:a. Trung điểm của một đoạn thẳng là tâm đối xứng của đoạn thẳng đó.b. Giao điểm hai đường chéo của một hình bình hành là tâm đối xứng của hình bình hành đó.c. Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.d. Tâm của một đường tròn là tâm đối xứng của đường tròn đó.
Đọc tiếp
Xét tính đúng – sai của mỗi khẳng định sau:
a. Trung điểm của một đoạn thẳng là tâm đối xứng của đoạn thẳng đó.
b. Giao điểm hai đường chéo của một hình bình hành là tâm đối xứng của hình bình hành đó.
c. Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.
d. Tâm của một đường tròn là tâm đối xứng của đường tròn đó.
Cho hình vẽ:
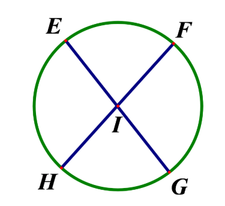
I là tâm của hình tròn này. Đúng hay sai?
A. Đúng
B. Sai
Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai?
A. AC + BD CD B. AC . BD
R
2
C.
O
D
2
DB. (AC + DB) D. Có 2 khẳng định sai
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB. Dựng các tiếp tuyến Ax và By với đường tròn. Lấy điểm I bất kì trên nửa đường tròn, tiếp tuyến tại I cắt Ax, By lần lượt tại C và D. Khẳng định nào sau đây là sai?
A. AC + BD = CD
B. AC . BD = R 2
C. O D 2 = DB. (AC + DB)
D. Có 2 khẳng định sai
Đáp án D
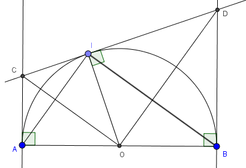
* Do AC và CI là 2 tiếp tuyến cắt nhau tại C nên: CA = CI ( tính chất 2 tiếp tuyến cắt nhau)
* Do BD và DI là 2 tiếp tuyến cắt nhau tại D nên: DB = DI ( tính chất 2 tiếp tuyến cắt nhau).
Suy ra: AC + BD = CI + DI = CD.
+) AC.BD = CI.DI (1)
Xét tam giác COD vuông tại O có đường cao OI nên:
CI.ID = I O 2 = R 2 (2)
Từ (1) và (2) suy ra: AC.BD = R 2
Và O D 2 = DI.DC = DB . (AC + BD)
Đúng 0
Bình luận (0)
Cho hai đường tròn bằng nhau có tâm lấn lượt là O, O’, biết chúng tiếp xúc ngoài, một phép quay tâm I và góc quay
π
2
biến đường tròn (O) thành đường tròn (O). Khẳng định nào sau đây sai? A. I nằm trên đường tròn đường kính OO’. B. I nằm trên đường trung trực đoạn OO’. C. I là giao điểm của đường tròn đường kính OO’ và trung trực đoạn OO’ D. Có hai tâm I của phép quay thỏa mãn điều kiện đầu bài.
Đọc tiếp
Cho hai đường tròn bằng nhau có tâm lấn lượt là O, O’, biết chúng tiếp xúc ngoài, một phép quay tâm I và góc quay π 2 biến đường tròn (O) thành đường tròn (O'). Khẳng định nào sau đây sai?
A. I nằm trên đường tròn đường kính OO’.
B. I nằm trên đường trung trực đoạn OO’.
C. I là giao điểm của đường tròn đường kính OO’ và trung trực đoạn OO’
D. Có hai tâm I của phép quay thỏa mãn điều kiện đầu bài.
Lập phương trình đường tròn trong mỗi trường hợp sau:
a) Đường tròn có tâm I(- 3 ; 4) bán kính R = 9;
b) Đường tròn có tâm I(5 ;-2) và đi qua điểm M(4;- 1);
c) Đường tròn có tâm I(1;- 1) và có một tiếp tuyến là A: 5x- 12y – 1 = 0;
d) Đường tròn đường kính AB với A(3;-4) và B(-1; 6);
e) Đường tròn đi qua ba điểm A(1;1), B(3; 1), C(0; 4).
a) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)
b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}} = \sqrt 2 \)
Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)
c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)
d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)
Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}} = \sqrt {29} \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)
e) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\) b
Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)
Đúng 0
Bình luận (0)