Cho hàm số y = x 3 + a x 2 + bx+1
Tìm a và b để đồ thị của hàm số đi qua hai điểm: A(1;2)và B(-2;-1)
Đồ thị hàm số đi qua A(1; 2) và B(-2; -1)
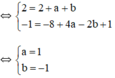
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực(đi qua điểm (1;0) và có điểm cực trị (-2; 0) . Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.
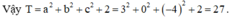
Cho hàm số f x = x 3 + a x 2 + b x + c thỏa mãn c > 2019 , a + b + c - 2018 < 0 . Số điểm cực trị của hàm số y = f x - 2019 là
Cho hàm số y = x 3 + ax 2 + bx + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. ab = 9
C. a = 0
D. a = 3b
Cho hàm số y = x 3 + a x 2 + b x + c b < 0 . Biết rằng đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt đối xứng qua gốc tọa độ. Giá trị của T=2(ab-c)+3 là:
A. T=3
B. T=1
C. T=2
D. T=5
Cho hàm số y = x 3 + ax 2 + bx + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3 b
D. ab = 9
Cho hàm số y = x 3 + a x 2 + b x + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3b
D. ab = 9
Đáp án D
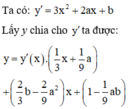
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
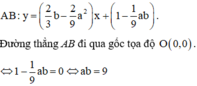
Cho hàm số y = x 3 + a x 2 + b x + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3b
D. ab = 9
Đáp án D
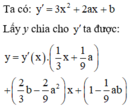
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
