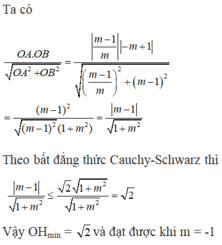Tìm m để khoảng cách từ O(0;0) đến đường thẳng (d) có phương trình y = (2m-1)x + 4m - 3 là lớn nhất và tìm khoảng cách lớn nhất đó.

Những câu hỏi liên quan
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Bạn viết sai rồi, đường thẳng y-mx+2 =0 hay y=mx+2 vậy bạn?
cho đường thẳng (d): y=m(2x-1)+3-2x
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng 1.
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) đạt giá trị lớn nhất.
Cho đường thẳng (d): y-mx+2
a) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) lớn nhất
b) tìm m để khoảng cách từ gốc tọa độ (O) đến (d) bằng 1
Cho đường thẳng có phương trình y=(m-2)x+2 tìm m để
a) khoảng cách từ 0 đến d bằng 1
b) khoảng cách từ o đến d lớn nhất
c) d cắt 2 trục tọa độ tạo thành 1 tam giác cso diện tích bằng 2
Tìm m để khoảng cách tù gốc tọa độ O đến đường thẳng d: y = mx - m +1 (m ≠ 0)
A. m = -1+ 2
B. m = 2
C. m = 2
D. m = -1
1)tính khoảng cách từ O đến đường thẳng d biết y=-2x+6
2)cho hàm số y=-mx+m-1(d) tìm m để khoảng cách từ O đến (d) là căn 3
ai giúp em giải với ạ em cảm ơn trước
a.
Gọi A là giao điểm của d với Ox \(\Rightarrow-2x_A+6=0\Rightarrow x_A=3\)
\(\Rightarrow OA=\left|x_A\right|=3\)
Gọi B là giao điểm của d với Oy \(\Rightarrow y_B=-2.0+6=6\)
\(\Rightarrow OB=\left|y_B\right|=6\)
Kẻ OH vuông góc AB \(\Rightarrow OH=d\left(O;d\right)\)
Áp dụng hệ thức lượng trong tam giác vuông OAB:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{9}+\dfrac{1}{36}=\dfrac{5}{36}\)
\(\Rightarrow OH=\dfrac{6\sqrt{5}}{5}\)
Đúng 1
Bình luận (0)
b.
Với \(m=0\Rightarrow y=-1\Rightarrow\) k/c từ O tới d là 1 (ktm)
Với \(m=1\Rightarrow y=-x\) đi qua O nên k/c từ O tới d bằng 0 (ktm)
Với \(m\ne\left\{0;1\right\}\):
Gọi A là giao điểm của d với Ox \(\Rightarrow-mx_A+m-1=0\Rightarrow x_A=\dfrac{m-1}{m}\)
\(\Rightarrow OA=\left|x_A\right|=\left|\dfrac{m-1}{m}\right|\)
Gọi B là giao điểm của d với Oy \(\Rightarrow y_B=-m.0+m-1=m-1\)
\(\Rightarrow OB=\left|y_B\right|=\left|m-1\right|\)
Trong tam giác vuông OAB, kẻ OH vuông góc AB \(\Rightarrow OH=d\left(O;d\right)\)
\(\Rightarrow OH=\sqrt{3}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\Leftrightarrow\dfrac{1}{3}=\dfrac{m^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Rightarrow3\left(m^2+1\right)=\left(m^2-1\right)\)
\(\Leftrightarrow m^2+m+1=0\) (vô nghiệm)
Vậy ko tồn tại m thỏa mãn yêu cầu
Đúng 1
Bình luận (0)
Cho hàm sô y = 2x + m − 3 có đồ thị là đường thằng (d) (với m là tham sỗ).
a) Tìm m đề khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng √5.
b) Tìm m để khoảng cách từ gốc tọa độ O đến đường thăng (d) nhỏ nhất.
Cho (d): y=x+m-4. Tìm m để khoảng cách từ O đến (d) lớn nhất
Tìm m để khoảng cách từ O đến đường thẳng d bằng 1 biết (d):y=(m-2)x+m+1
Xem chi tiết
Với \(m=-1\) thì d qua O nên k/c bằng 0 (loại), với \(m=2\) thì đường thẳng (d) có dạng \(y=3\) nên k/c từ O đến (d) bằng 3 (loại)
Với \(m\ne\left\{-1;2\right\}\)
Gọi A và B lần lượt là giao điểm của (d) với Ox và Oy
\(\Rightarrow x_A=-\dfrac{m+1}{m-2}\) ; \(y_B=m+1\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_A\right|=\left|\dfrac{m+1}{m-2}\right|\\OB=\left|y_B\right|=\left|m+1\right|\end{matrix}\right.\)
Gọi H là chân đường cao hạ từ O xuống d \(\Rightarrow OH\) là đường cao trong tam giác vuông OAB (vuông tại O) đồng thời \(OH=1\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\Leftrightarrow1=\left(\dfrac{m-2}{m+1}\right)^2+\dfrac{1}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(m+1\right)^2=\left(m-2\right)^2+1\)
\(\Leftrightarrow6m=4\)
\(\Rightarrow m=\dfrac{2}{3}\)
Đúng 2
Bình luận (0)