Trong không gian Oxy cho hai mặt phẳng (P); x-3y+2z+1=0 , (Q): (2m-1)x+m(1-2m)y+ (2m-4)z+14=0. Tìm m để (P) (Q) vuông góc với nhau
A. m ∈ 1 ; - 3 2
B. m ∈ 1 ; 3 2
C. m ∈ - 1 ; - 3 2
D. m ∈ 2
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:
A. y+z=0 và y-z=0
B. x+y=0 và x-y=0
C. x+z=0 và x-z=0
D. y+2z=0 và y-2z=0
Đáp án A
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
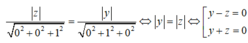
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:
A. 2x - 4 = 0
B. y - 6 = 0
C. z + 3 = 0
D. 2x - 6y - 3z - 49 = 0
Đáp án B
Vì (P) vuông góc với hai mặt phẳng (Oxy), (Oyz) và (Oxy) (Oyz) = Oy nên ta có (P) → Oy => n p → = j → = (0; 1; 0)
Từ đó suy ra phương trình của mặt phẳng (P) là: 0(x - 2) + 1(y - 6 ) + 0(z + 3) = 0 ⇔ y - 6 = 0
Trong không gian Oxyz, cho hai điểm A 1 ; 2 ; 1 , B 2 ; − 1 ; 3 . Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 − 2 M B 2 lớn nhất.
A. M(3;-4;0)
B. M 3 2 ; 1 2 ; 0
C. M(0;0;5)
D. M 1 2 ; − 3 2 ; 0
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 − 2 M B 2 lớn nhất.
A. M 0 ; 0 ; 5 .
B. M 1 2 ; − 3 2 ; 0 .
C. M 3 ; − 4 ; 0 .
D. M 3 2 ; 1 2 ; 0 .
Đáp án C
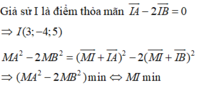
Suy ra M là hình chiếu vuông góc của I lên (Oxy) => I(3;-4;0)
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A. M 0 ; 0 ; 5
B. M 1 2 ; - 3 2 ; 0
C. M 3 ; - 4 ; 0
D. M 3 2 ; 1 2 ; 0
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
![]()
![]()
Đáp án A.
Cách giải:
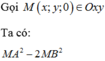
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm M(1;1;1) và vuông góc với hai mặt phẳng (Oxy),(Ozx).
A. y-1=0.
B. x-1=0.
C. z-1=0.
D. x+z-2=0.
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A . M 3 2 ; 1 2 ; 0
B . M 1 2 ; - 3 2 ; 0
C. M (0; 0; 5)
D. M (3; -4; 0)
Trong không gian với hệ tọa độ Oxy cho mặt phẳng P : 2 x - y - z + 1 = 0 và hai điểm A 2 ; 1 ; 1 , B 3 ; 3 ; 2 . Điểm M a ; b ; c với b > 0 nằm trong mặt phẳng (P) sao cho O M ⊥ A B và M A = 26 . Giá trị của tổng a + b + c bằng.
A. 1
B. 3
C. -2
D. 5
Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán để xác định tọa độ điểm M.
Cách giải: Ta có:

Trong không gian với hệ tọa độ Oxy, cho mặt phẳng P : - 2 x + y - 3 z + 1 = 0 Một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()