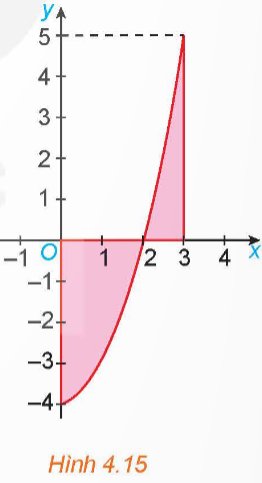
Tính diện tích hình phẳng giới hạn bởi parabol y = x2 – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).
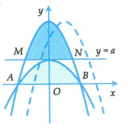
Cho parabol P 1 : y = - x 2 + 2 x + 3 cắt trục hoành tại hai điểm A, B và đường thẳng d : y = a 0 < a < 4 . Xét parabol P 2 đi qua A, B và có đỉnh thuộc đường thẳng y = a . Gọi S 1 là diện tích hình phẳng giới hạn bởi P 1 và d. S 2 là diện tích hình phẳng giới hạn bởi P 2 và trục hoành. Biết S 1 = S 2 , tính T = a 3 - 8 a 2 + 48 a .
A. T = 99
B. T = 64
C. T = 32
D. T = 72
Chọn đáp án B
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương trình các parabol mới là
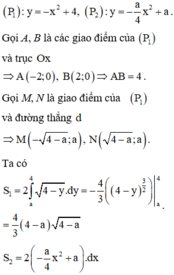
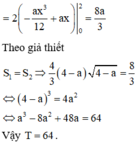
Cho hàm số y = x 2 - m x ( 0 < m < 4 ) có đồ thị (C). Gọi S 1 là diện tích hình phẳng giới hạn bởi (C) và trục hoành; S 2 là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x=m,x=4. Biết S 1 = S 2 , giá trị của m bằng
A. 10 3 .
B. 2.
C. 3.
D. 8 3 .
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
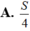
![]()
![]()
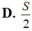
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
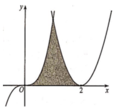
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 , đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H)
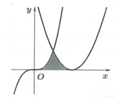
A. S = 11 2
B. S = 7 2
C. S = 20 3
D. S = - 11 2
Hoành độ giao điểm của (C) và (P) là nghiệm phương trình: ![]()
Hoành độ giao điểm của (P) và Ox là nghiệm phương trình:
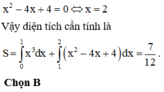
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H).
A. S = 11 2
B. S = 7 12
C. S = 20 3
D. S = - 11 2
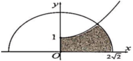
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 với 0 ≤ x ≤ 2 2 , nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 3 π + 14 6
B. 3 π + 2 3
C. 3 π + 4 3
D. c
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 với ( 0 ≤ x ≤ 2 2 ) nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
![]()
![]()
![]()
![]()
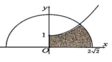
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 (với 0 ≤ x ≤ 2 2 ), nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 3 π + 14 6
B. 2 π + 2 3
C. 3 π + 4 6
D. 3 π + 2 3
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 32 3
C. 9
D. 5 3
Đáp án C
Phương trình hoành độ giao điểm hai đồ thị là
