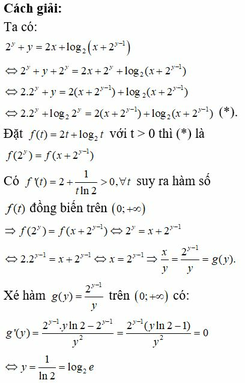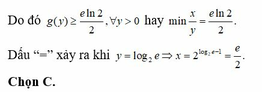Cho hai số x, y thỏa mãn x-2y=5; x^2+4y^2=29. Tính giá trị của A =x^3-8y^3

Những câu hỏi liên quan
Cho hai số tự nhiên x,y thỏa mãn: (x-3)(2y+5)=74. Tập hợp các giá trị y thỏa mãn là{...}
cho hai số x, y thỏa mãn x-2y=5 và x^2+4y^2=29
Cho x,y là hai số thỏa mãn x+2y=3. Tìm GTNN của E= x^2 +2y^2
Từ x + 2y =3 => x = 3 - 2y.Thay x = 3 -2y vào biểu thức E ,ta có :
E = x2 +2y2 =(3-2y)2 + 2y2 =6y2 -12y + 9
= \(6.\left(y^2-2y+\frac{3}{2}\right)=6.\left[\left(y^2-2y+1\right)+\frac{1}{2}\right]=6.\left[\left(y-1\right)^2+\frac{1}{2}\right]=6\left(y-1\right)^2+3\)
Do (y-1)2 \(\ge\)0=> E\(\ge\)3.
Vậy MINE khi y = 1,x =3 - 2.1 =1
x+2y=3⇒y=3−x2⇒y=3−x2(1)
Thế (1) vào E ta được : E=x22+x2−6x+92x2−6x+92
⇔2E=2x2+x2−6x+9⇔2E=3x2−6x+9⇔2E=2x2+x2−6x+9⇔2E=3x2−6x+9
⇔2E=3(x2−2x+1+2)⇔E=32[(x−1)2+2]⇔2E=3(x2−2x+1+2)⇔E=32[(x−1)2+2]
⇔E=32(x−1)2+3⇔E=32(x−1)2+3 . Do (x-1)22≥≥0⇒32(x−1)2≥0⇒32(x−1)2≥0⇒32(x−1)2+3≥3⇔E≥3⇒32(x−1)2+3≥3⇔E≥3 . Hay Emin=3Emin=3 .
Vậy giá trị nhỏ nhất của E là 3 ⇔{x=1y=1
Cho hai số thực dương x, y thỏa mãn
2
y
+
y
2
x
+
log
2
(
x
+
2
y
-
1
)
.
Giá trị nhỏ nhất của biểu thức
P
x
y
bằng A.
e
+...
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn 2 y + y = 2 x + log 2 ( x + 2 y - 1 ) . Giá trị nhỏ nhất của biểu thức P = x y bằng
A. e + ln 2 2
B. e - ln 2 2
C. e ln 2 2
D. e 2 ln 2
Cho hai số thực dương x,y, thỏa mãn: 2016/x + 1=2016/y và x + 2y = 7056/3. Tính x/y
Thì ra cx có ng k hiểu thầy nói gì giống mình
Đúng 0
Bình luận (0)
Cho hai số nguyên dương x, y thỏa mãn x 2 +y 2 +2x(y−1) +2y+1 là số chính phương. Chứng minh rằng x = y
Xét \(P=x^2+y^2+2x\left(y-1\right)+2y+1\)
\(P=x^2+y^2+2xy-2x+2y+1\)
+) Nếu \(y>x\) thì \(2y-2x+1>0\). Do đó \(P>\left(x+y\right)^2\). Hơn nữa:
\(P< x^2+y^2+1+2xy+2x+2y\) \(=\left(x+y+1\right)^2\),
suy ra \(\left(x+y\right)^2< P< \left(x+y+1\right)^2\), vô lí vì P là SCP.
+) Nếu \(x>y\) thì \(2y-2x+1< 0\) nên \(P< \left(x+y\right)^2\)
Hơn nữa \(P>x^2+y^2+1+2xy-2x-2y\) \(=\left(x+y-1\right)^2\)
Suy ra \(\left(x+y-1\right)^2< P< \left(x+y\right)^2\), vô lí vì P là SCP.
Vậy \(x=y\) (đpcm)
(Cơ mà nếu thay \(x=y\) vào P thì \(P=4x^2+1\) lại không phải là SCP đâu)
Đúng 1
Bình luận (0)
Cho hai số dương x,y thỏa mãn x > y và (x-2y)2 /xy=8/3. Tính x/y
1)Tìm tất cả các cặp số nguyên x,y thỏa mãn : x2=y(y+1)(y+2)(y+3)
2)Cho các số nguyên x,y,z thỏa mãn S=x+2y+3z+2016 và P=(x+2015)5+(2y-2016)5+(3z+2017)5
Mk đang cần gấp . Mơn mấy thím trc
Cho hai số thực x,y thỏa mãn \(x+y\le1\). Tìm GTNN của
\(M=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\sqrt{1+x^2y^2}\)
Lời giải:
Áp dụng BĐT AM-GM:
$M\geq 2\sqrt{\frac{1}{xy}}.\sqrt{1+x^2y^2}=2\sqrt{\frac{x^2y^2+1}{xy}}$
$=2\sqrt{xy+\frac{1}{xy}}$
Áp dụng BĐT AM-GM tiếp:
$1\geq x+y\geq 2\sqrt{xy}\Rightarrow xy\leq \frac{1}{4}$
$xy+\frac{1}{xy}=(xy+\frac{1}{16xy})+\frac{15}{16xy}$
$\geq 2\sqrt{xy.\frac{1}{16xy}}+\frac{15}{16xy}$
$\geq 2\sqrt{\frac{1}{16}}+\frac{15}{16.\frac{1}{4}}=\frac{17}{4}$
$\Rightarrow M\geq 2\sqrt{\frac{17}{4}}=\sqrt{17}$
Vậy $M_{\min}=\sqrt{17}$. Giá trị này đạt tại $x=y=\frac{1}{2}$
Đúng 1
Bình luận (0)